In DisPerSE, structures are identified as components of the Morse-Smale complex of an input function defined over a - possibly bounded - manifold. The Morse-Smale complex of a real valued so-called Morse function is a construction of Morse theory which captures the relationship between the gradient of the function, its topology, and the topology of the manifold it is defined over.

Figure 1: the Morse-Smale complex

Upper left: critical points (minima, saddle points and maxima pictured as blue, green and red disks), and three integral lines (pink curves) of a Morse function. Black arrows show the gradient of that function. Upper right: ascending 2-manifolds : the set of points belonging to integral lines whose destination is the same minimum (critical point of index 0). Lower left: descending 2-manifolds : the set of points belonging to integral lines whose origin is the same maximum (critical point of index 2). Lower right: the Morse-Smale complex : a natural tesselation of space into cells induced by the gradient fo the function. Each cell is the set of points belonging to integral lines whose origin and destination are identical (i.e. each cell is the intersection of an ascending and a descending manifold). The purple region is a 2-cell: intersection of an ascending and a descending 2-manifold (red and blue regions) where all field lines have the same orgin and destination (a minimum and a maxium). The yellow curve is a 1-cell (also called an arc): the intersection of and ascending 2-manifold (blue region) and a descending 1-manifolds (green+yellow curves, originating from the same saddle point).

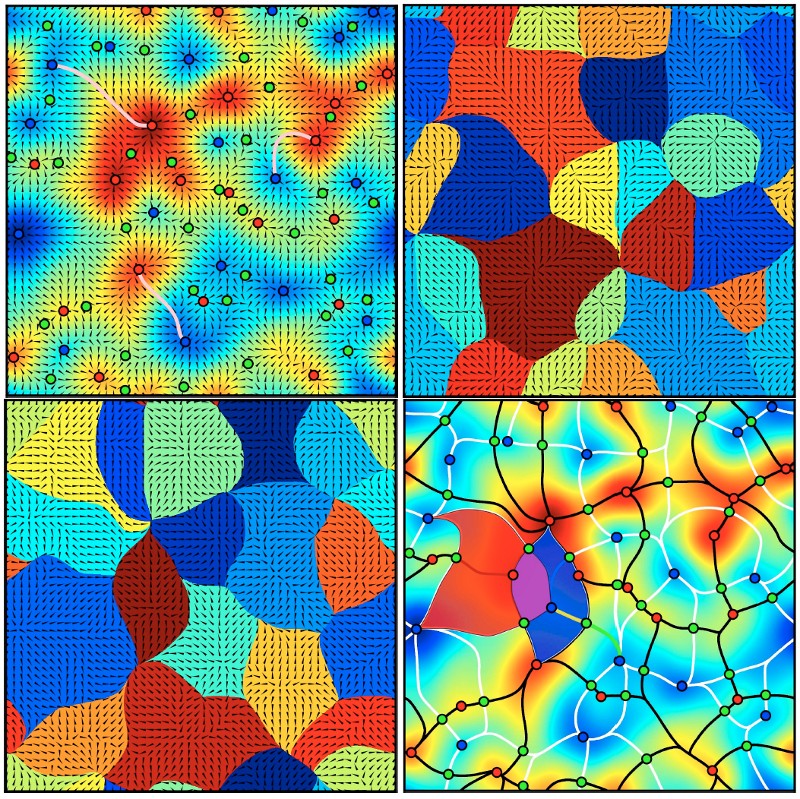
Two central notions in Morse theory are that of critical point and integral line (also called field line) : (see the upper left frame of figure 1)

• -Critical points are the discrete set of points where the gradient of the function is null. For a function defined over a 2D space, there are three types of critical points (4 in 3D, ...), classified by their critical index. In 2D, minima have a critical index of 0, saddle points have a critical index of 1 and maxima have a critical index of 2. In 3D and more, different types of saddle points exist, one for each non extremal critical index.

• -Integral lines are curves tangent to the gradient field in every point. There exist exactly one integral line going through every non critical point of the domain of definition, and gradient lines must start and end at critical points (i.e. where the gradient is null).

Because integral lines cover all space (there is exactly one critical line going through every point of space) and their extremities are critical points, they induce a tessellation of space into regions called ascending (resp. descending) k-manifolds where all the field lines originate (respectively lead) from the same critical point (see ascending and descending 2-manifolds on figure 1, upper right and lower left panels). The number of dimensions k of the regions spanned by a k-manifold depend directly on the critical index of the corresponding critical point: descending k-manifolds originate from critical points of critical index k while the critical index is N-k for ascending manifolds, with N the dimension of space.

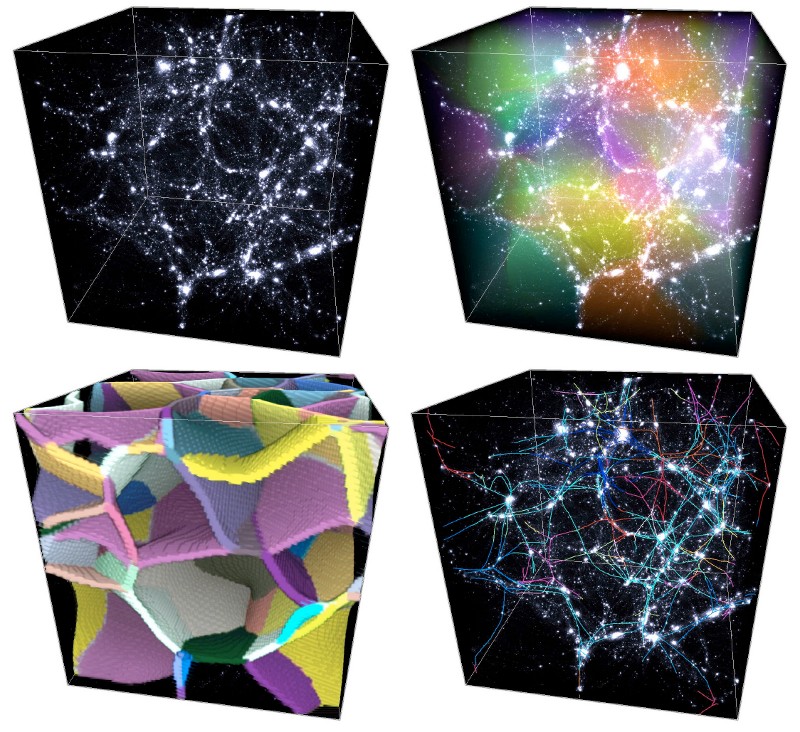
The set of all ascending (or descending) manifolds is called the Morse complex of the function. The Morse-Smale complex is an extension of this concept: the tessellation of space into regions called p-cells where all the integral lines have the same origin and destination (see figure 1, lower right frame). Each p-cell of the Morse-Smale complex is the intersection of an ascending and a descending manifold and the Morse-Smale complex itself is a natural tessellation of space induced by the gradient of the function. Figure 2 below illustrates how components of the Morse-Smale complex can be used to identify structures in a 3D distribution.

Figure 2: 3D structures identified as component of the Morse-Smale complex

Upper left: Density distribution of dark matter in a chunk of the Universe represented by tracer particles from a N-Body cosmological simulation. Upper right: Ascending 3-manifolds tracing the voids Lower left: Ascending 2-manifolds tracing the walls Lower right: The set of arcs with one maximum at their extremity, also called upper skeleton, tracing the filamentary structures. The maxima, not represented here, identify dark matter halos onto which filaments plug.