
Research
Secular resonant dressed orbital diffusion - I. Method and WKB limit for tepid discs
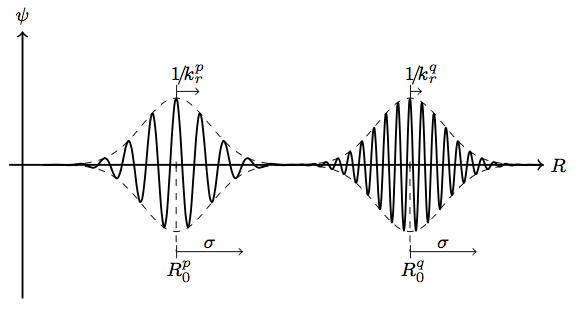
We derived the secular diffusion equation of a self-gravitating collisionless system induced by external stochastic perturbations. In the case of a tepid galactic disc, relying on the WKB assumption that only tightly wound transient spirals are sustained by the disc, we obtained a simple quadrature for the diffusion coefficients, providing a straightforward understanding of the loci of maximal diffusion.
We recovered the main orbital signatures of the secular evolution of an isolated self-gravitating stellar disc. The shot-noise-driven formation of narrow ridges of resonant orbits is recovered in the WKB limit of tightly wound transient spirals, in agreement with numerical simulations. This justifies the relevance of the dressed Fokker-Planck formalism in angle-action variables to describe the secular evolution of such systems.
Self-gravity, Resonances, and Orbital Diffusion in Stellar Disks
Fluctuations in a stellar system's gravitational field cause the orbits of stars to evolve. The resulting evolution of the system can be computed with the orbit-averaged Fokker-Planck equation. We presented the formalism that enables one to compute the diffusion tensor from a given source of noise when the system's gravitational dynamical response to that noise is included. This formalism, which recovers the formations of narrow ridges of enhanced density in action space, appears as the ideal framework in which to study the long-term evolution of all kinds of stellar discs.
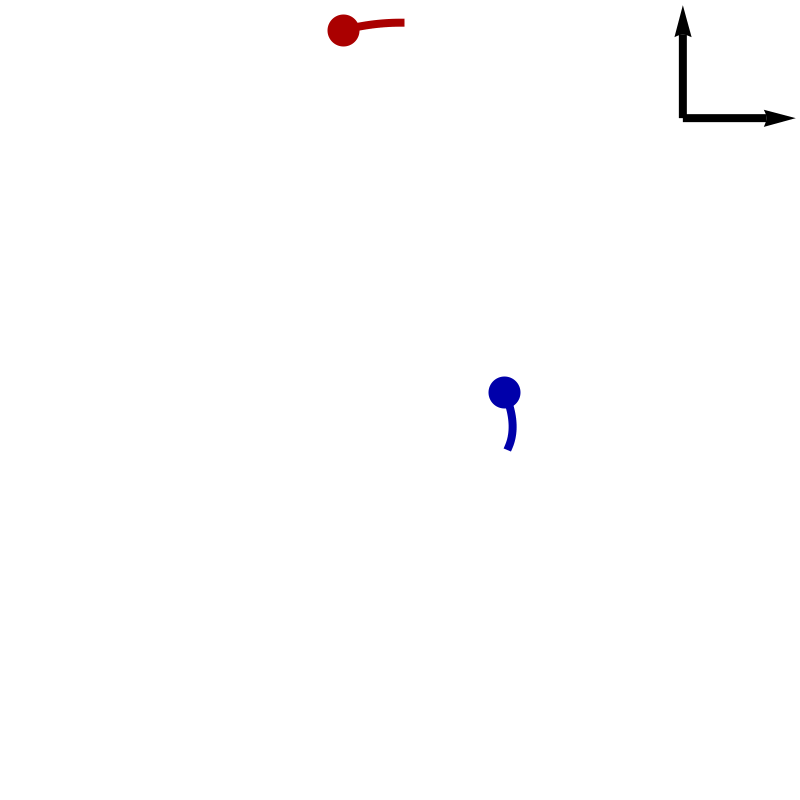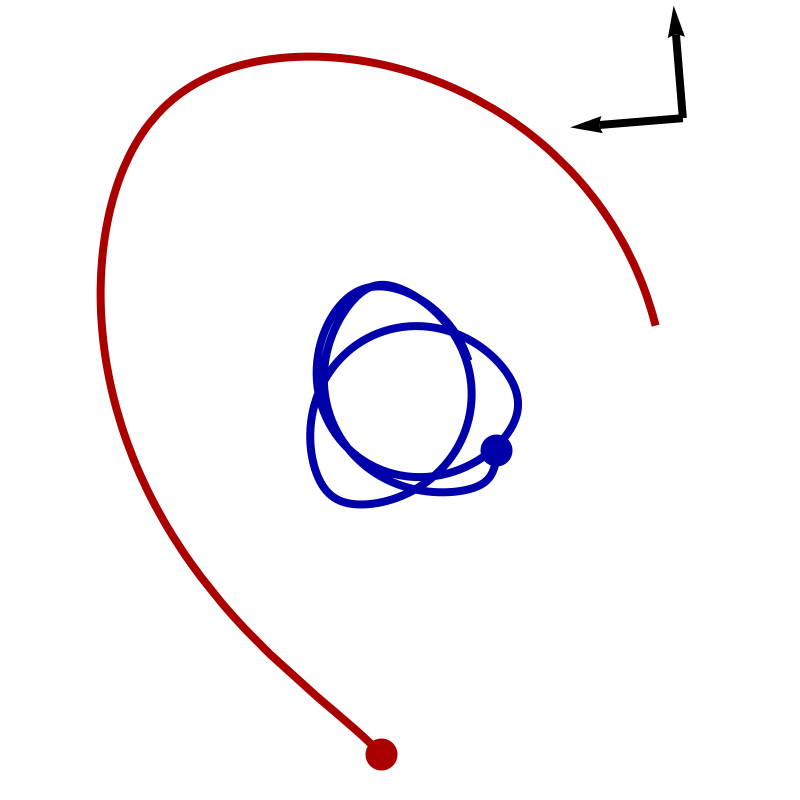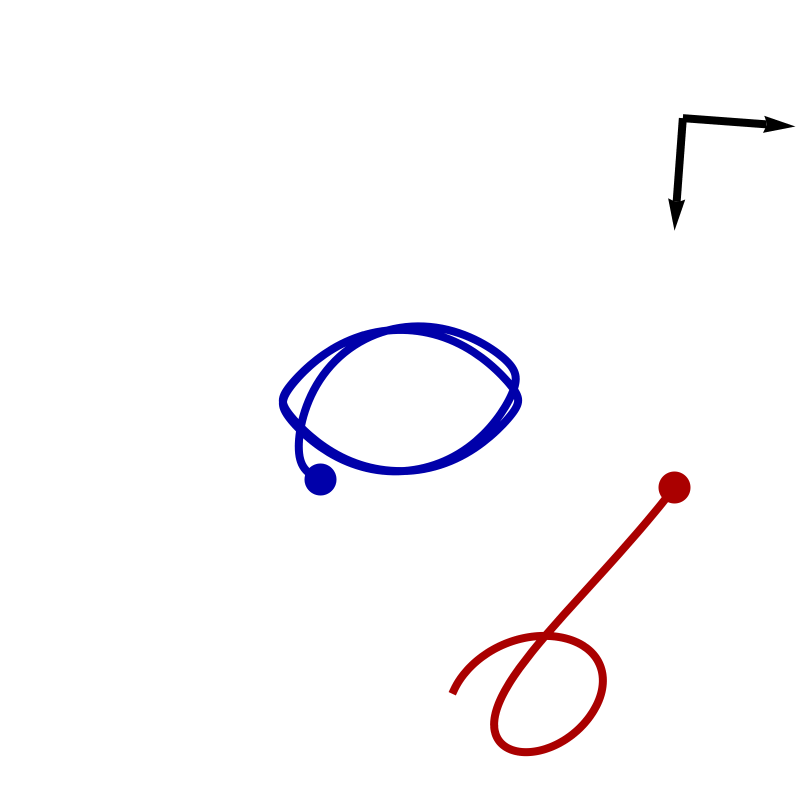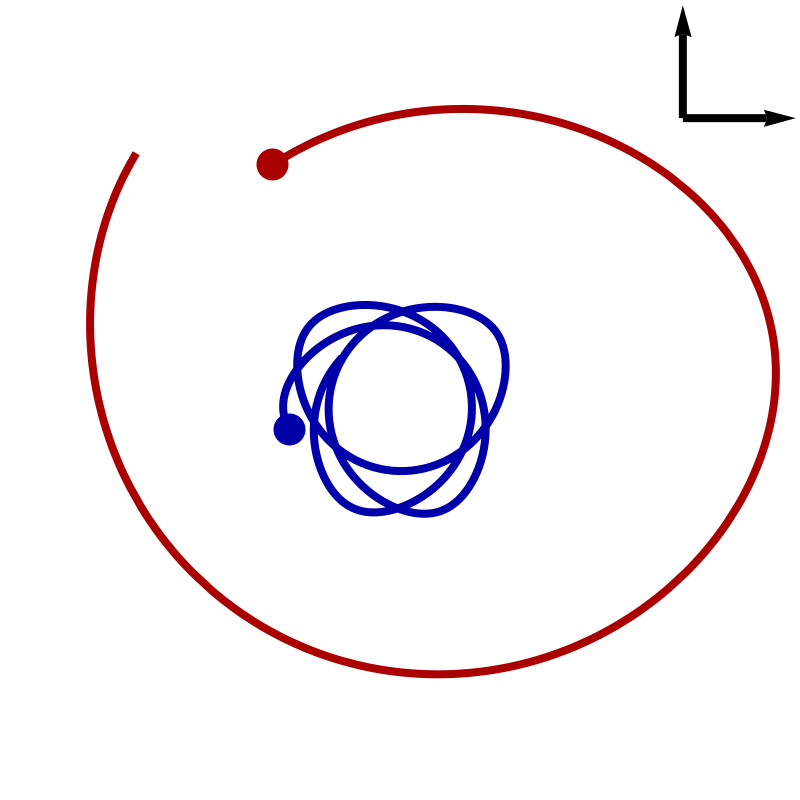
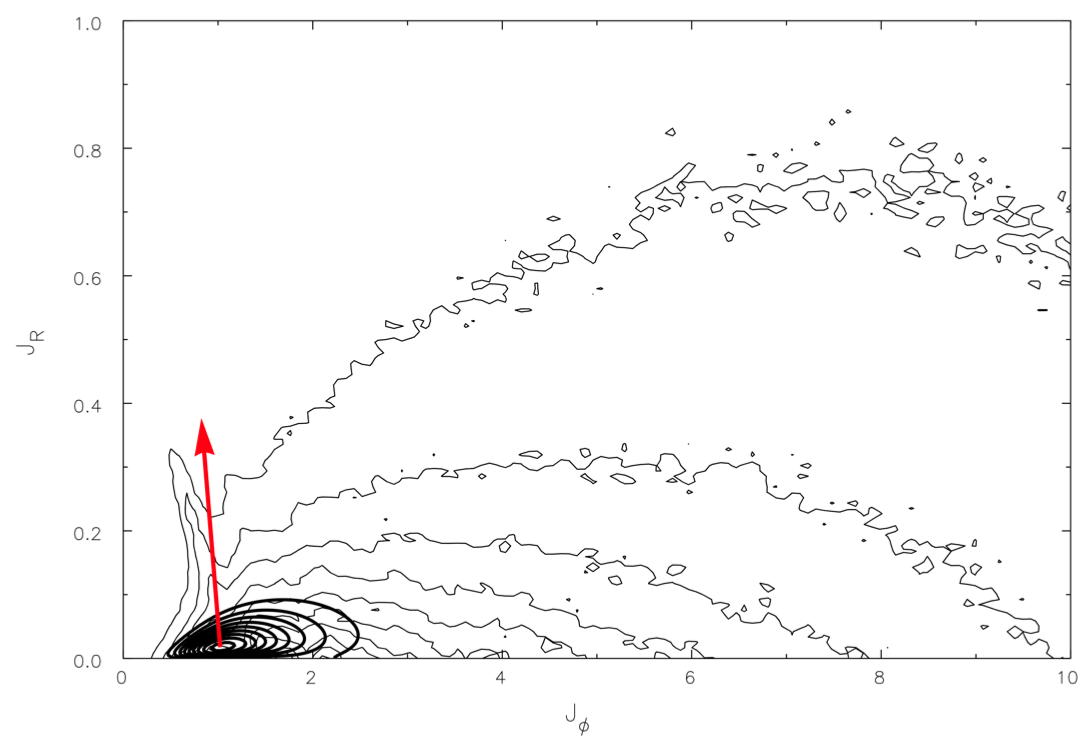
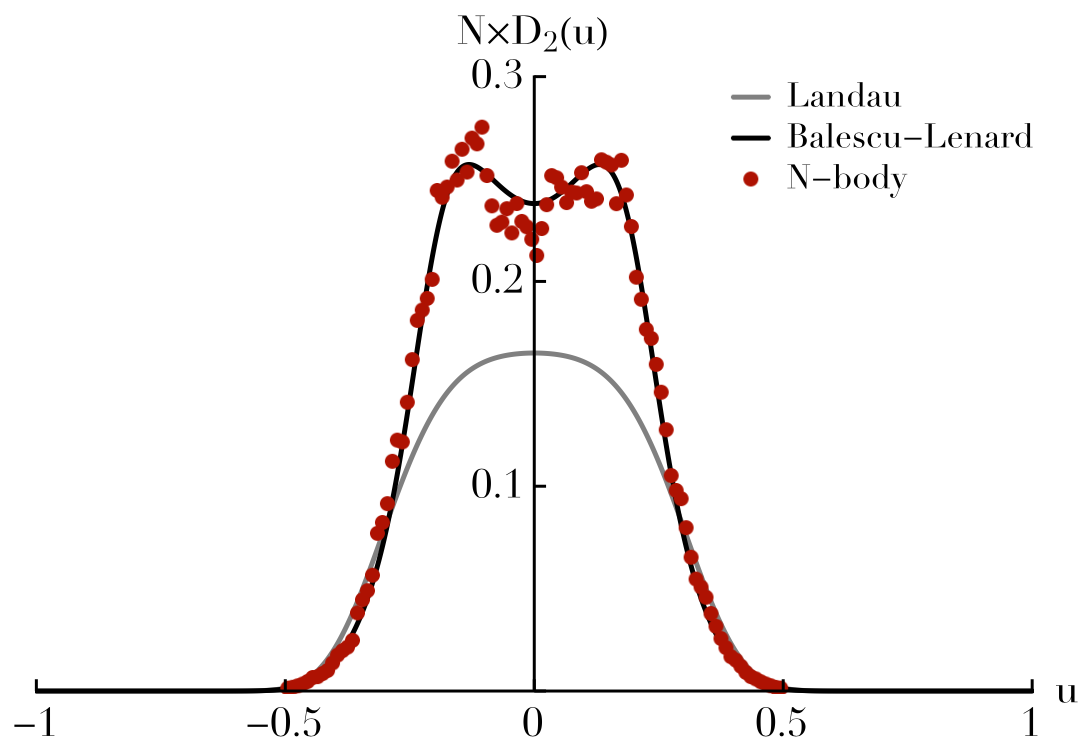
We described the secular evolution of an infinitely thin isolated discrete self-gravitating stellar disc using the inhomogeneous Balescu-Lenard equation. Assuming that only tightly wound transient spirals are present in the disc, a WKB approximation provides a simple quadrature for the corresponding drift and diffusion coefficients. When applied to the secular evolution of an isolated stationary discrete self-gravitating Mestel disc, it predicts the formation of a ridge-like feature in action space, in agreement with simulations, but over-estimates the timescale involved in its appearance. Swing amplification is needed to resolve this discrepancy.
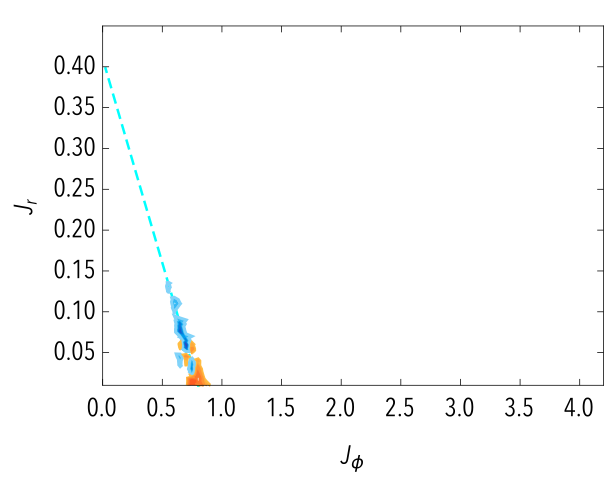
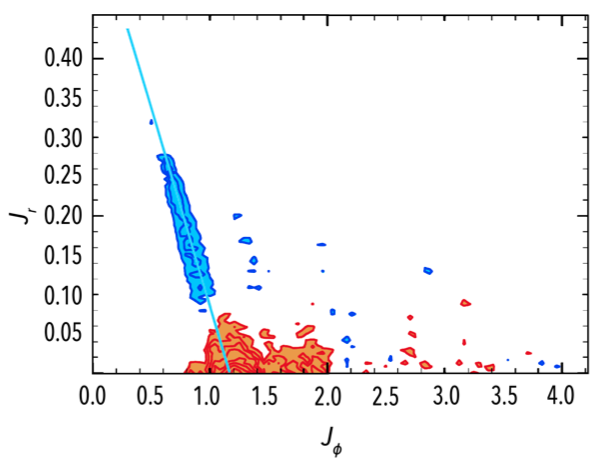
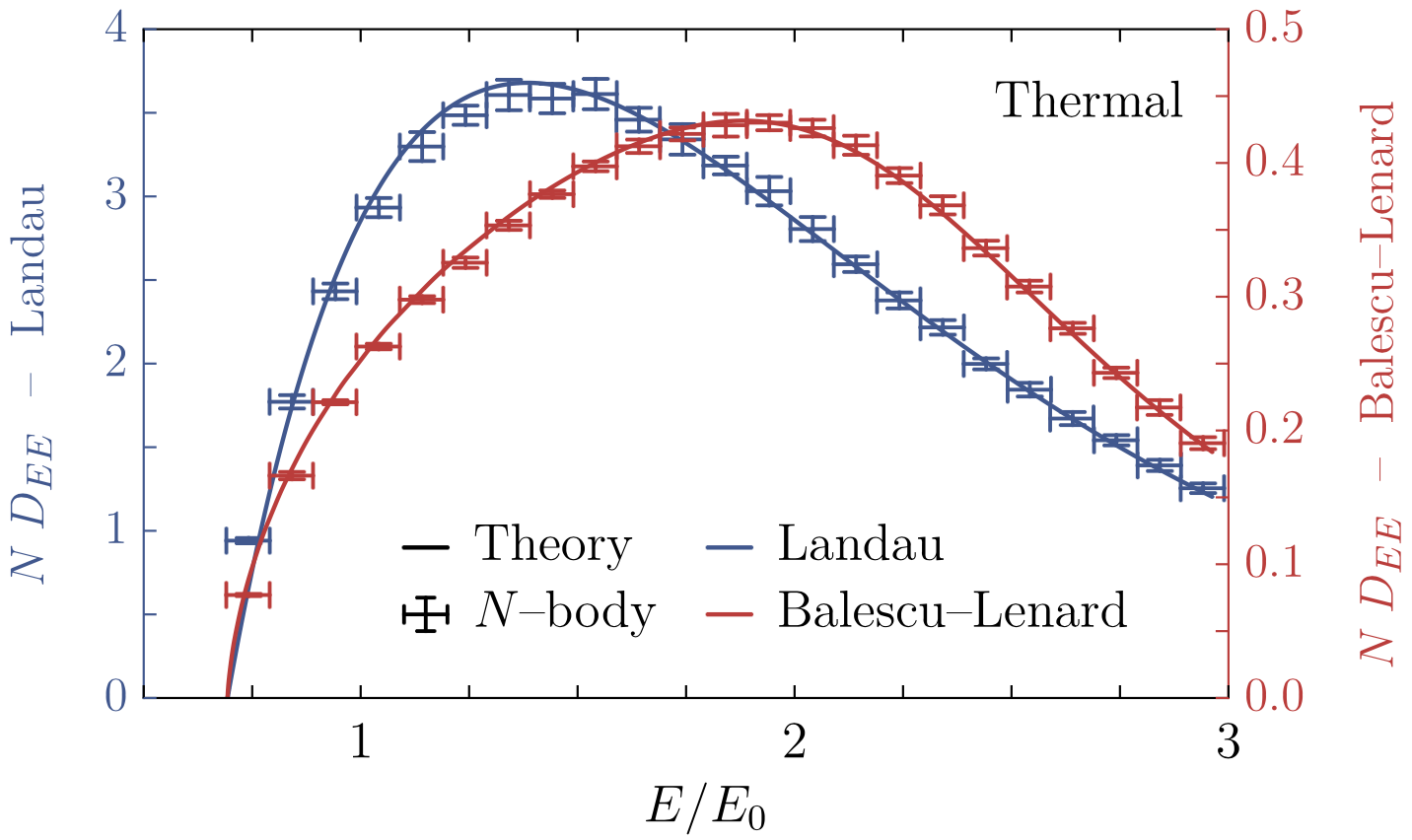
We investigated the secular evolution of an infinitely thin discrete self-gravitating stella disc using the inhomogeneous Balescu-Lenard equation in terms of angle-action variables. We implemented numerically the matrix method to capture the induced graviational polarisation. The position/shape of the induced resonant ridge are found to be in very good agreement with the numerical simulations, as well as the diffusion timescales. Quantitative comparisons with N-body simulations also yield consistent scalings with the number of particles.
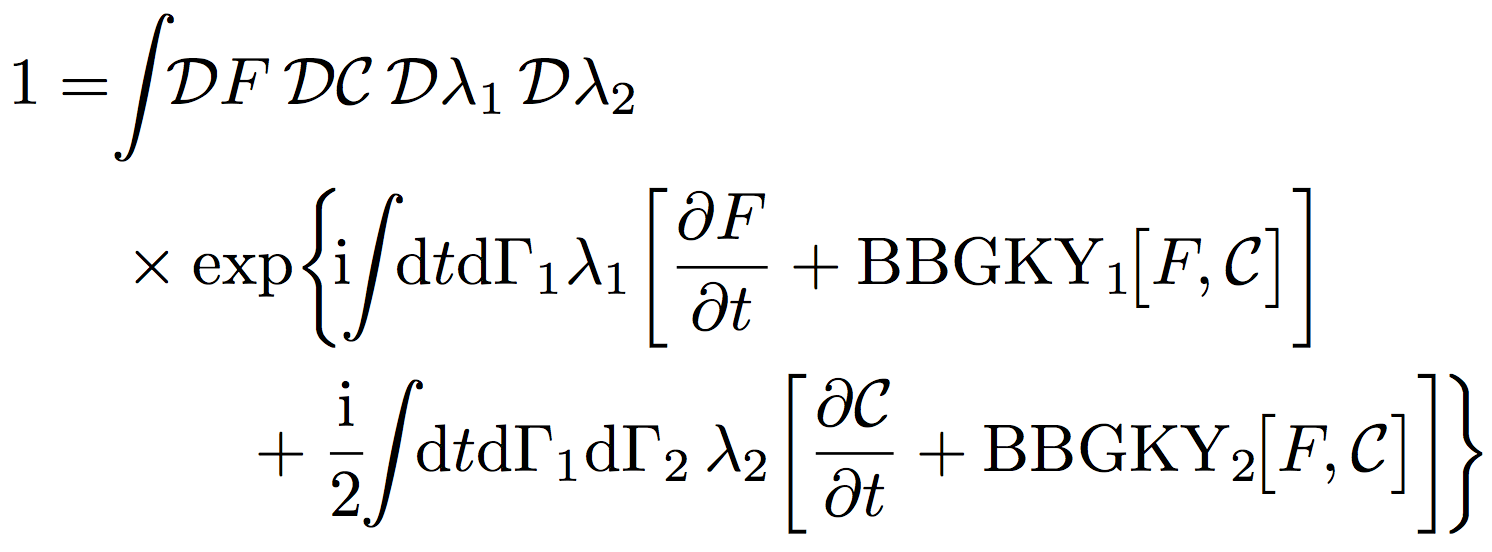
Functional integral approach to the kinetic theory of inhomogeneous systems
We present a derivation of the kinetic equation describing the secular evolution of spatially inhomogeneous systems with long-range interactions, the so-called inhomogeneous Landau equation, by relying on a functional integral formalism.
Functional integral derivation of the kinetic equation of two-dimensional point vortices
We present a brief derivation of the kinetic equation describing the secular evolution of point vortices in two-dimensional hydrodynamics, by relying on a functional integral formalism.
We derive the kinetic equation that describes the secular evolution of a large set of particles orbiting a dominant massive object, such as stars bound to a supermassive black hole or a proto-planetary debris disc encircling a star. This degenerate Balescu-Lenard equation describes self-consistently the long-term evolution of the distribution of quasi-Keplerian orbits around the central object: it is the master equation that describes the secular effects of resonant relaxation.
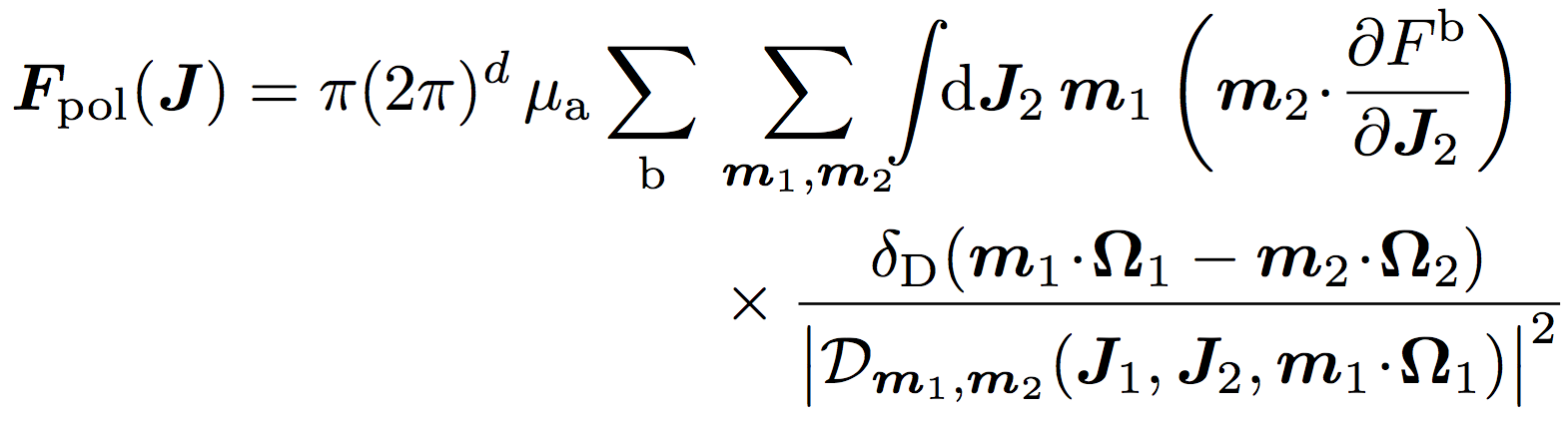
We derive general self-consistent expressions for the coefficients of diffusion and dynamical friction in a stable, bound, multicomponent, self-gravitating, and inhomogeneous system.

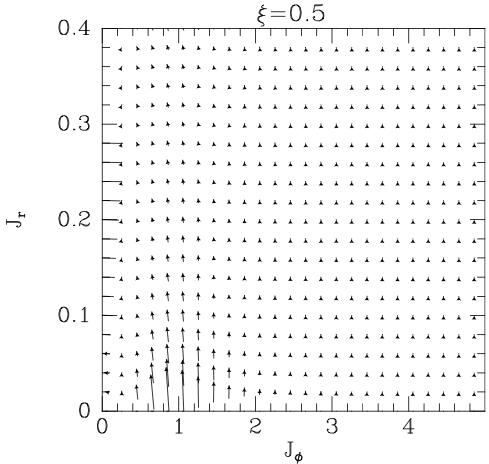
We investigate the secular thickening of a self-gravitating stellar galactic disc using the dressed collisionless Fokker-Planck equation and the inhomogeneous multi-component Balescu-Lenard equation, by relying on a generalised thickened WKB approximation. When applied to a tepid stable tapered disc perturbed by shot noise, these two frameworks predict the formation of ridges of resonant orbits towards larger vertical actions, as found in direct numerical simulations, but over-estimates the timescale involved in their appearance. Swing amplification is likely needed to resolve this discrepancy, as demonstrated in the case of razor-thin discs.
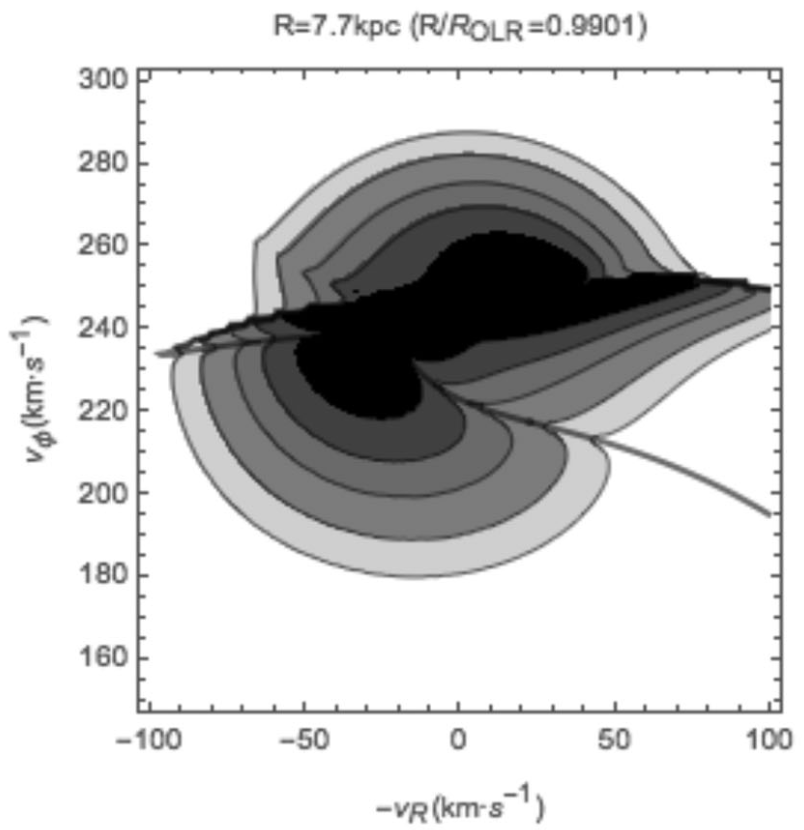
Distribution functions for resonantly trapped orbits in the Galactic disc
We show how to compute the response of the DF of a galactic disc to a bar-like perturbation in the region of orbit-trapping, where the traditional perturbation theory fails.
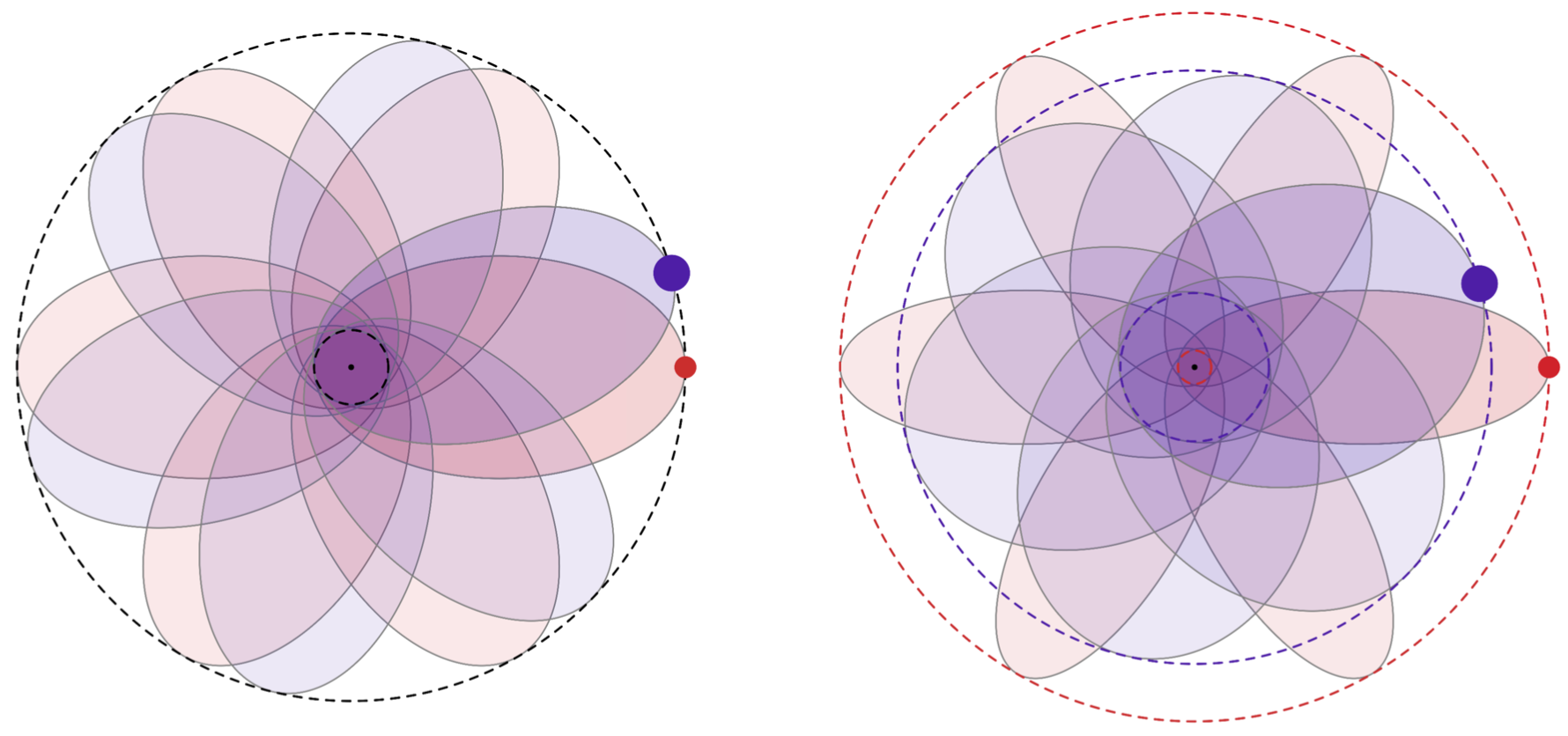
Relying on Gauss' method, we compute the drift and diffusion coefficients characterising the properties of the resonant relaxation of a razor-thin quasi-Keplerian disc.
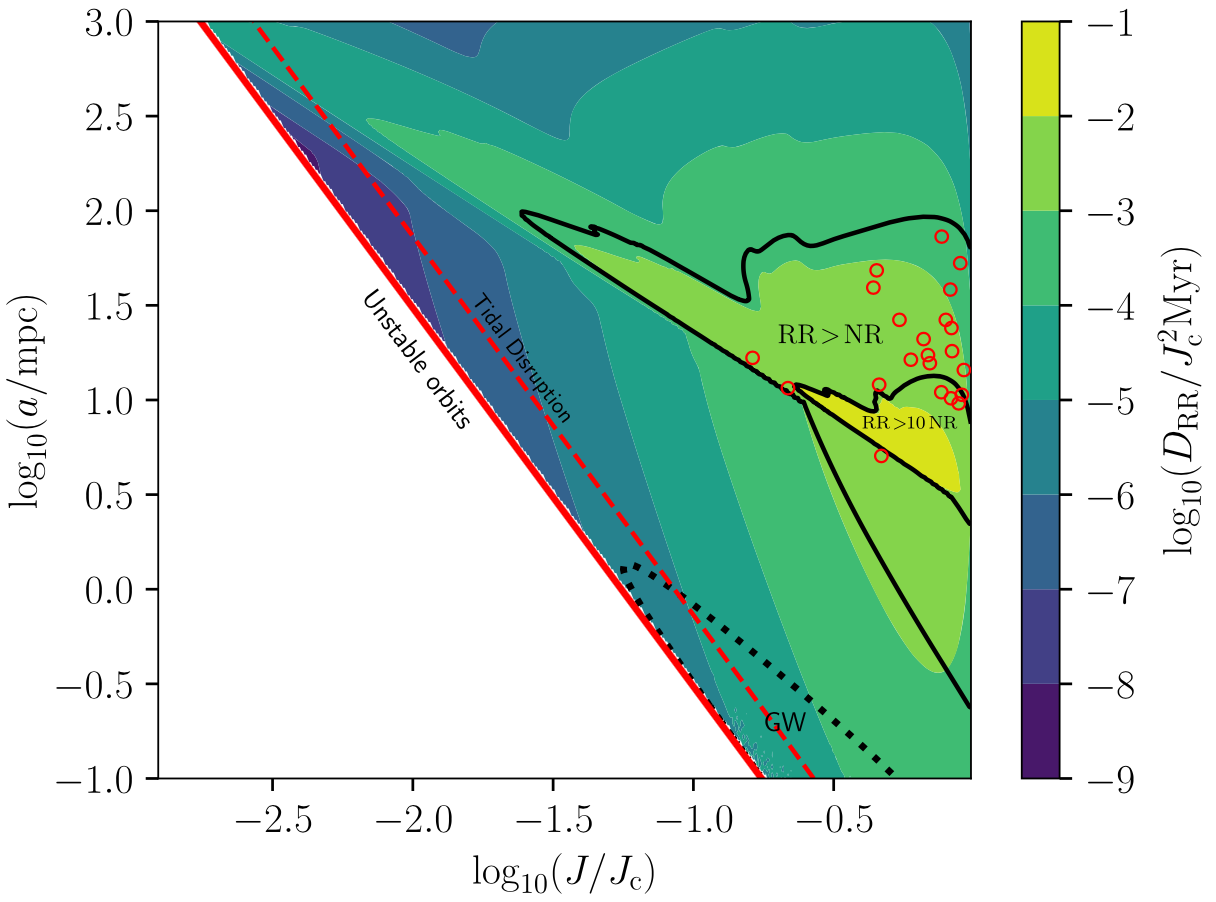
Scalar Resonant Relaxation of Stars around a Massive Black Hole
We describe from first principles the process of scalar resonant relaxation (relaxation of the norm of the angular momentum) in galactic nuclei.
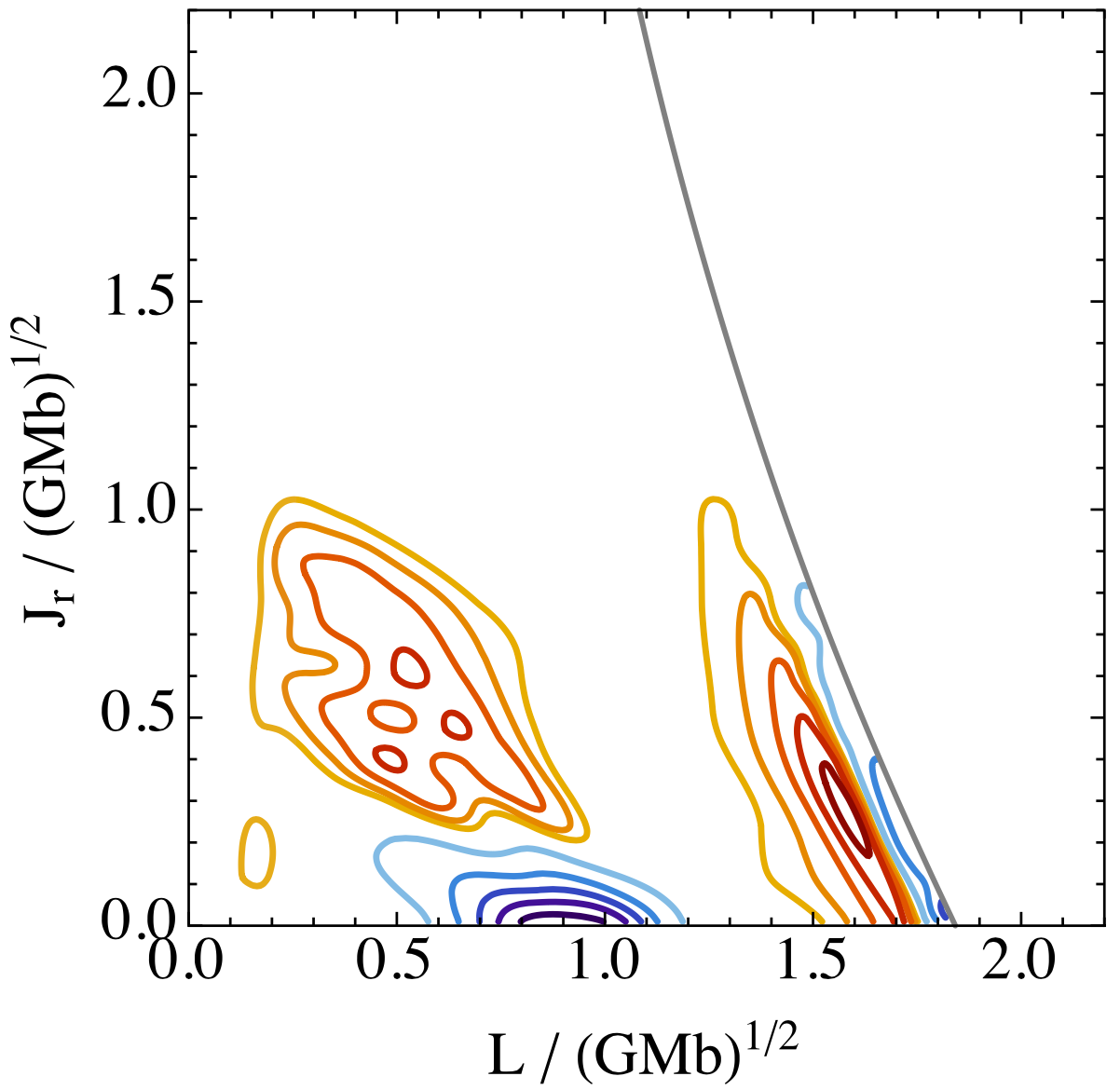
Revisiting relaxation in globular clusters
We adapt the Balescu-Lenard equation to spherical systems such as globular clusters. We use it to estimate the flux through action space, and compare it with classical theory.
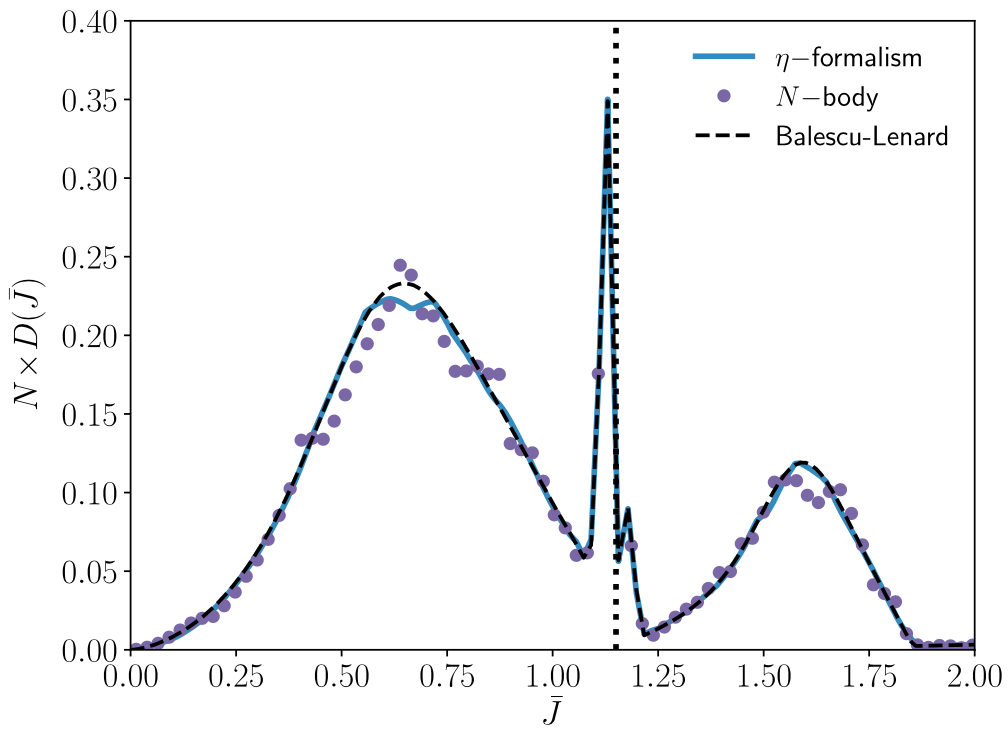
Relaxation in self-gravitating systems
We show how the stochastic η-formalism allows for the recovery of the Balescu-Lenard and Landau equations. This approach provides a new view of the resonant diffusion processes associated with long-term orbital distortions.
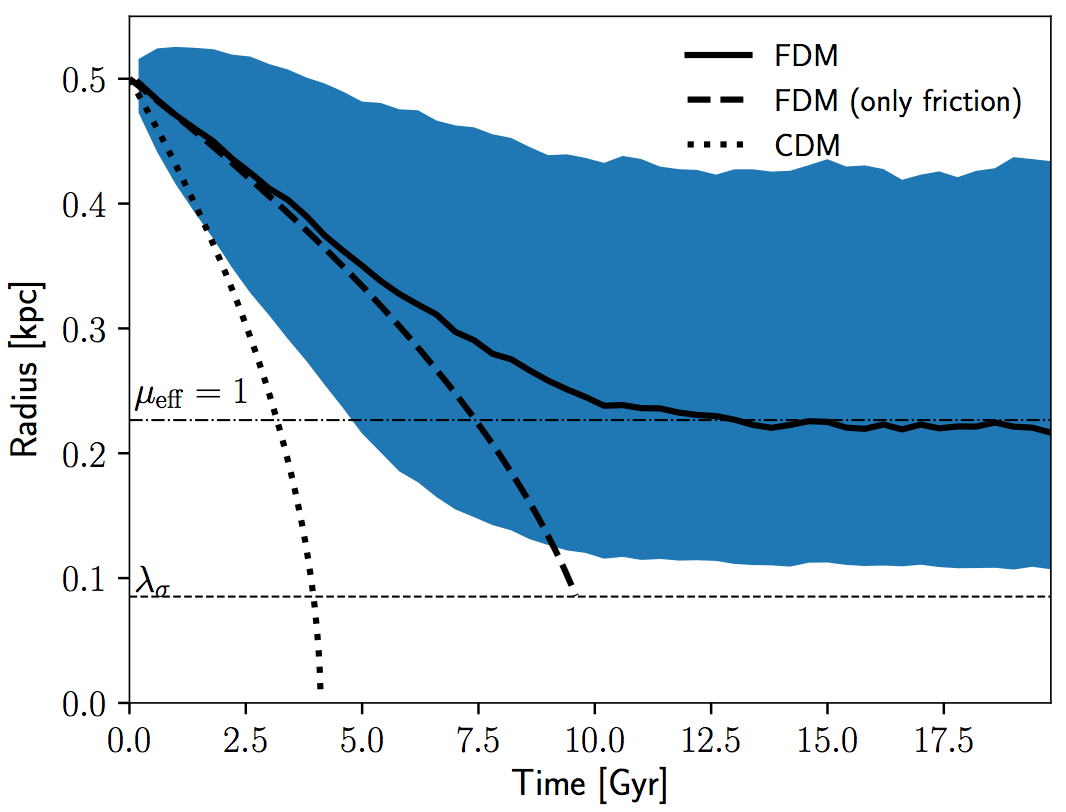
Relaxation in a Fuzzy Dark Matter Halo
By treating the FDM fluctuations as quasiparticles, we show how the relaxation in a FDM halo can be analysed quantitatively with the same tools used to analyse classical two-body relaxation in an N-body system.
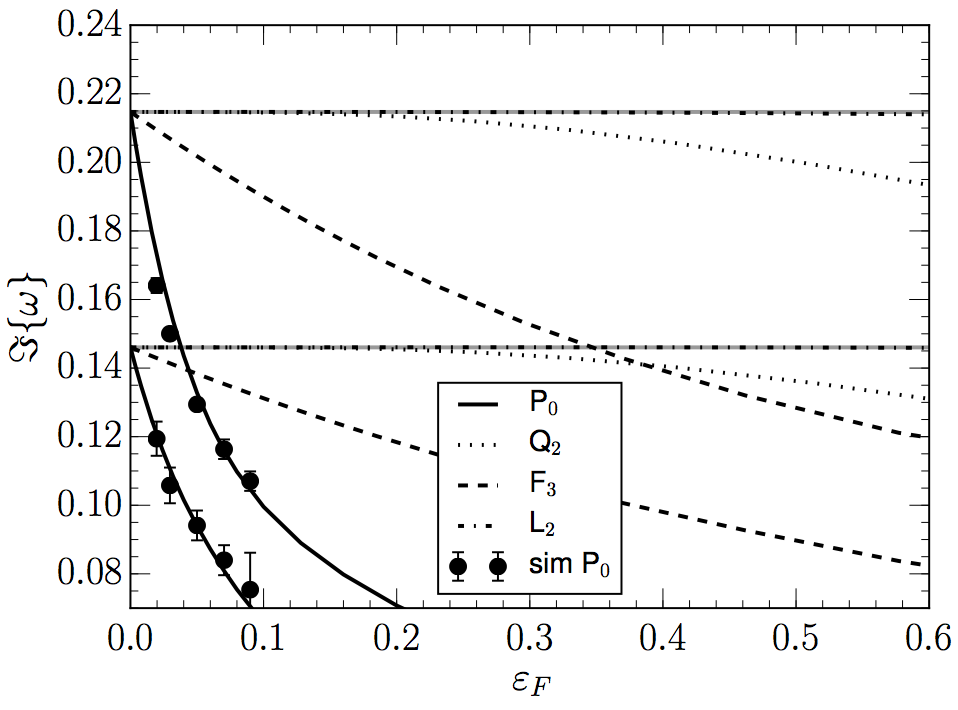
How gravitational softening affects galaxy stability. I. Linear mode analysis of disc galaxies
We use linear pertubation theory to investigate the effect of graviational softening on the spiral eigenmodes of razor-thin stellar discs.
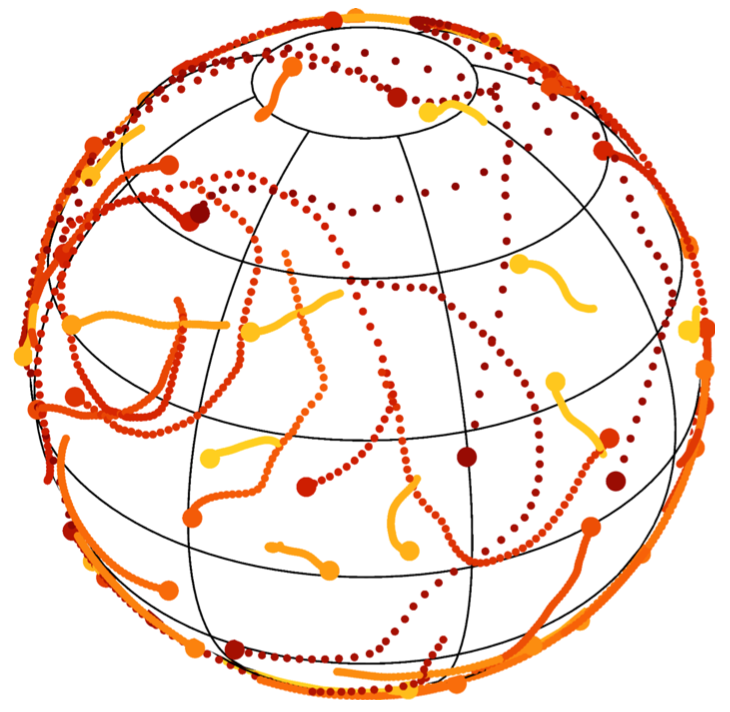
Secular dynamics of long-range interacting particles on a sphere in the axisymmetric limit
We investigate the secular dynamics of long-range interacting particles moving on a sphere, in the limit of an axisymmetric mean field potential.
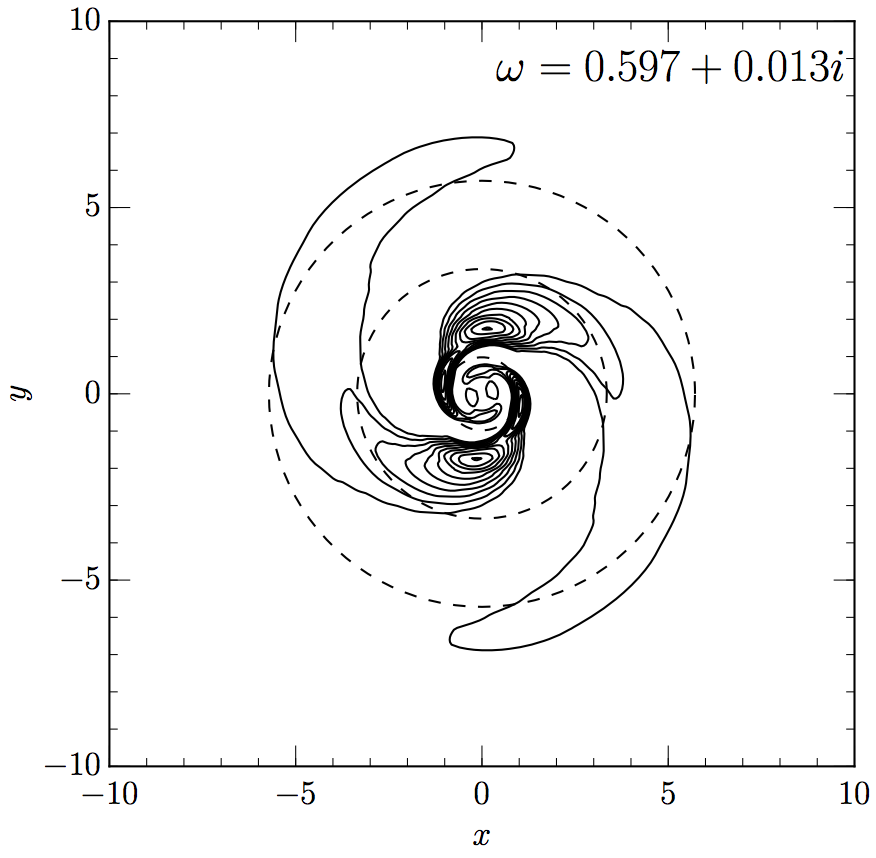
Instabilities in disc galaxies: from noise to grooves to spirals
Using linear response theory, we show how grooves in action space (spontaneously generated via finite-N effects) can lead unstable modes in razor-thin stellar discs.
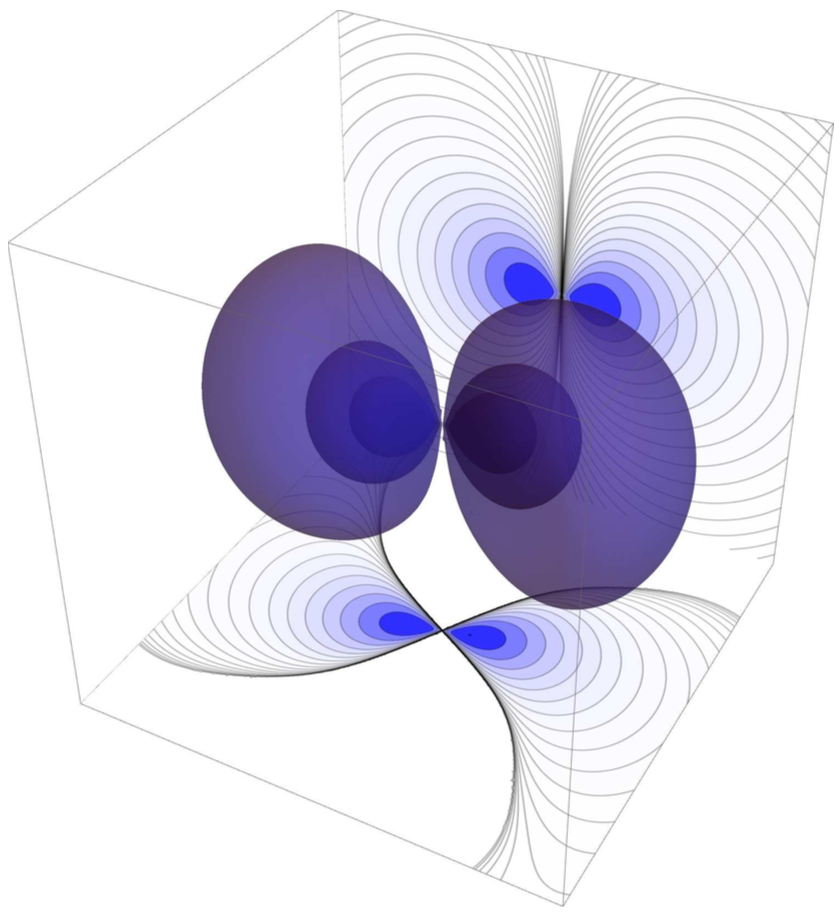
Mapping the stability of stellar rotating spheres via linear response theory
We investigate the linear stability of rotating stellar clusters with varying velocity anisotropies.
Vector Resonant Relaxation of Stars around a Massive Black Hole
We derive from first principles the statistical properties of random walks undergone by stellar orbital orientations in galactic nuclei.
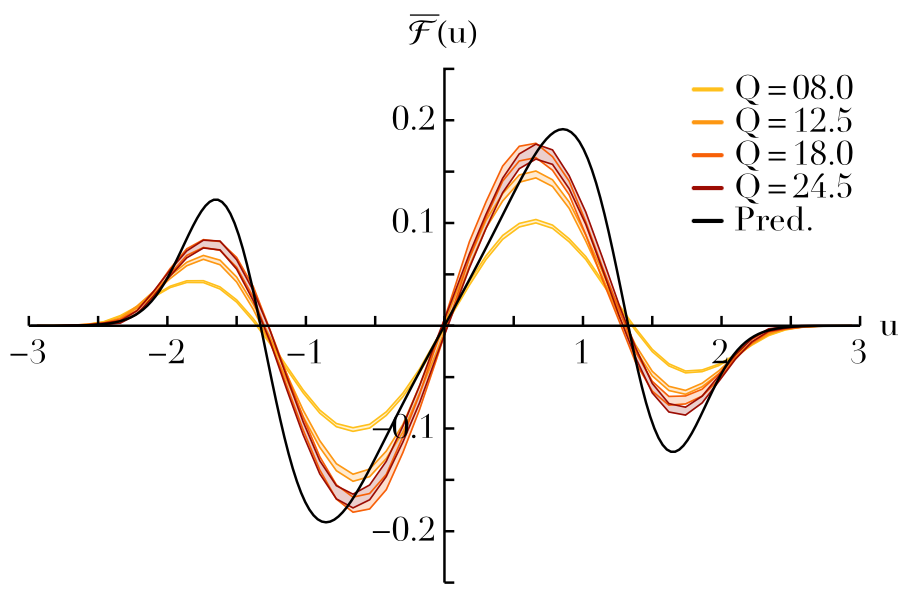
Kinetic theory of 1D homogeneous long-range interacting systems sourced by 1/N^2 effects
We present a 1/N^2 kinetic theory of the HMF model in the limit where collective effects can be neglected.
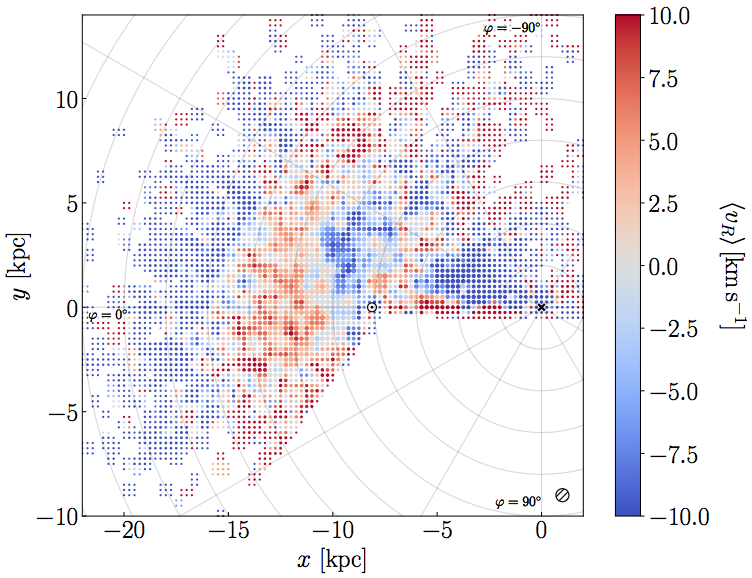
The Strength of the Dynamical Spiral Perturbation in the Galactic Disk
We characterise the amplitude of the spiral perturbation in the Milky Way.
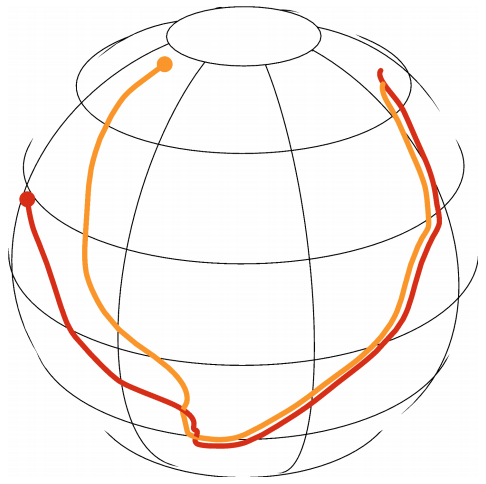
We develop the theory of "neighbor separation" for the vector resonant relaxation in galactic nuclei.
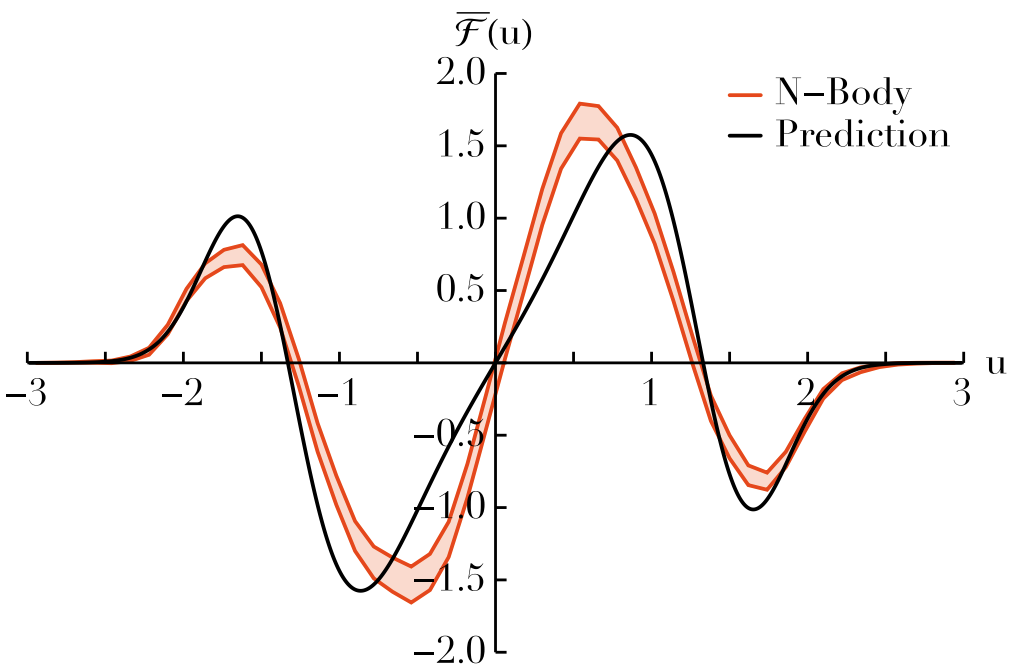
We develop the 1/N^2 kinetic theory of 1D homogeneous long-range interacting systems.
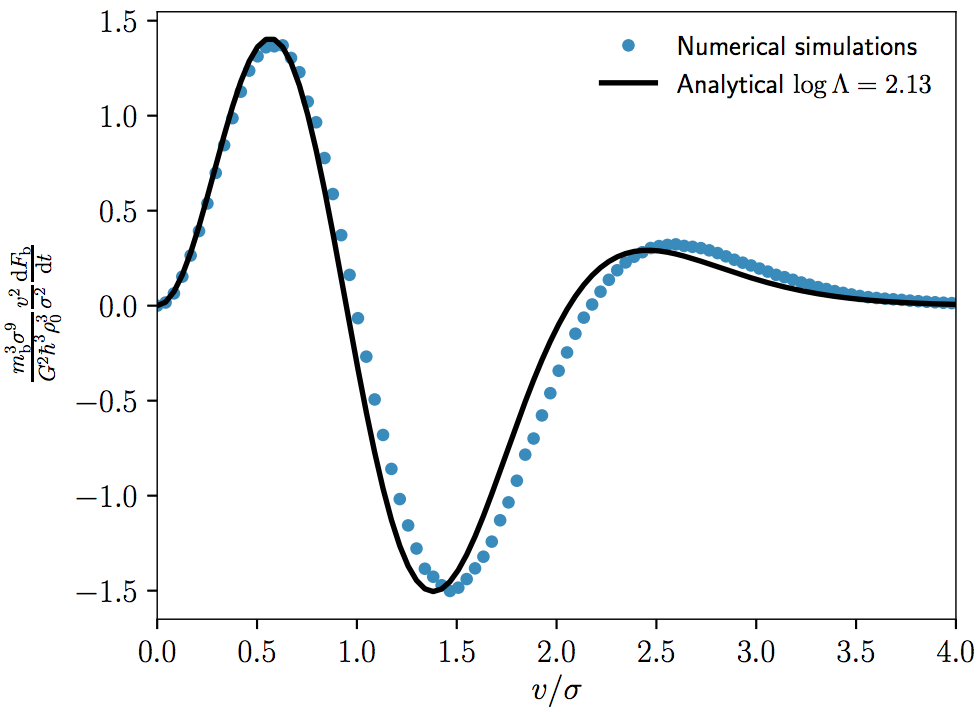
Relaxation in a Fuzzy Dark Matter Halo. II. Self-consistent kinetic equations
We derive a kinetic equation to describe the self-consistent relaxation of fuzzy dark matter halos.
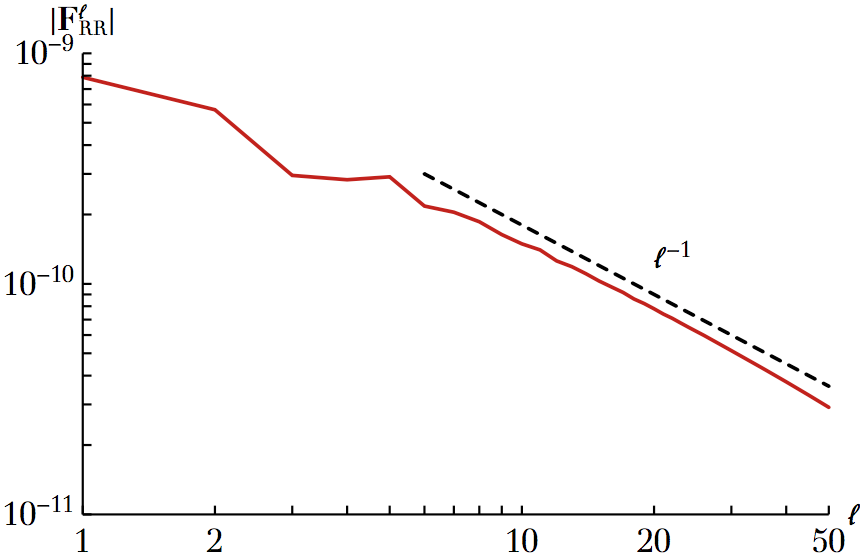
Resonant and non-resonant relaxation of globular clusters
We compute the diffusion rate in action space using both resonant and non-resonant kinetic theories. We compare with direct N-body measurements
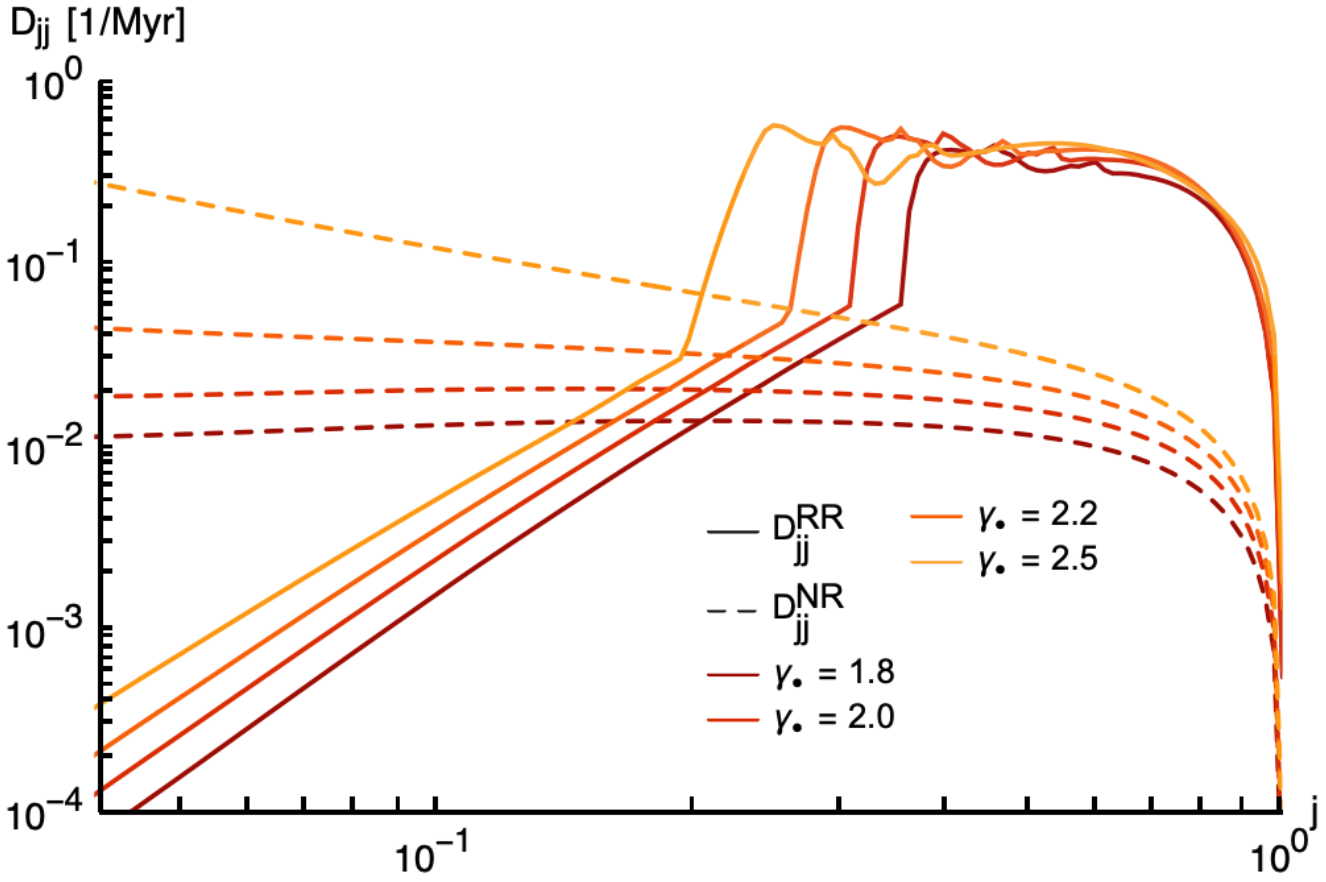
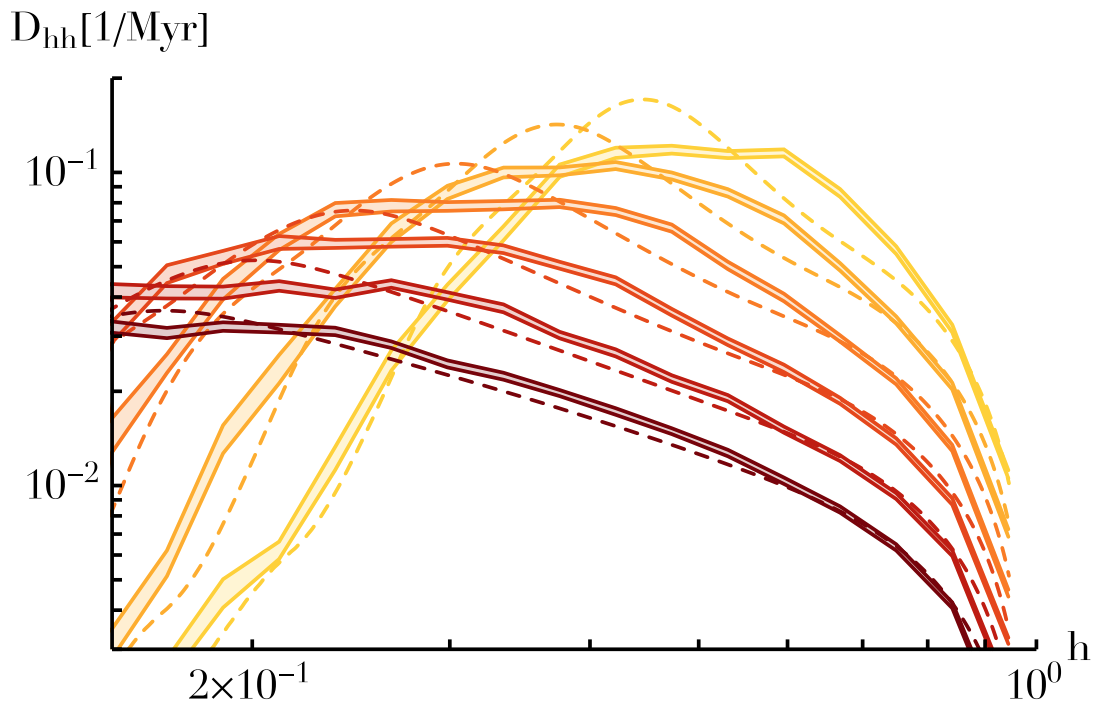
Mapping the Galactic centre's dark cluster via Resonant Relaxation
We use scalar resonant relaxation and the observed distribution of the S-stars' eccentricities to constrain the stellar content around SgrA*.
Secular Dynamics around a Supermassive Black Hole via Multipole Expansion
Within the secular approximation of smearing out stars along their underlying Keplerian orbits, we detail how a multipole expansion of the pairwise interaction between the stars yields an efficient numerical code to investigate the long-term evolution of stellar orbital parameters.
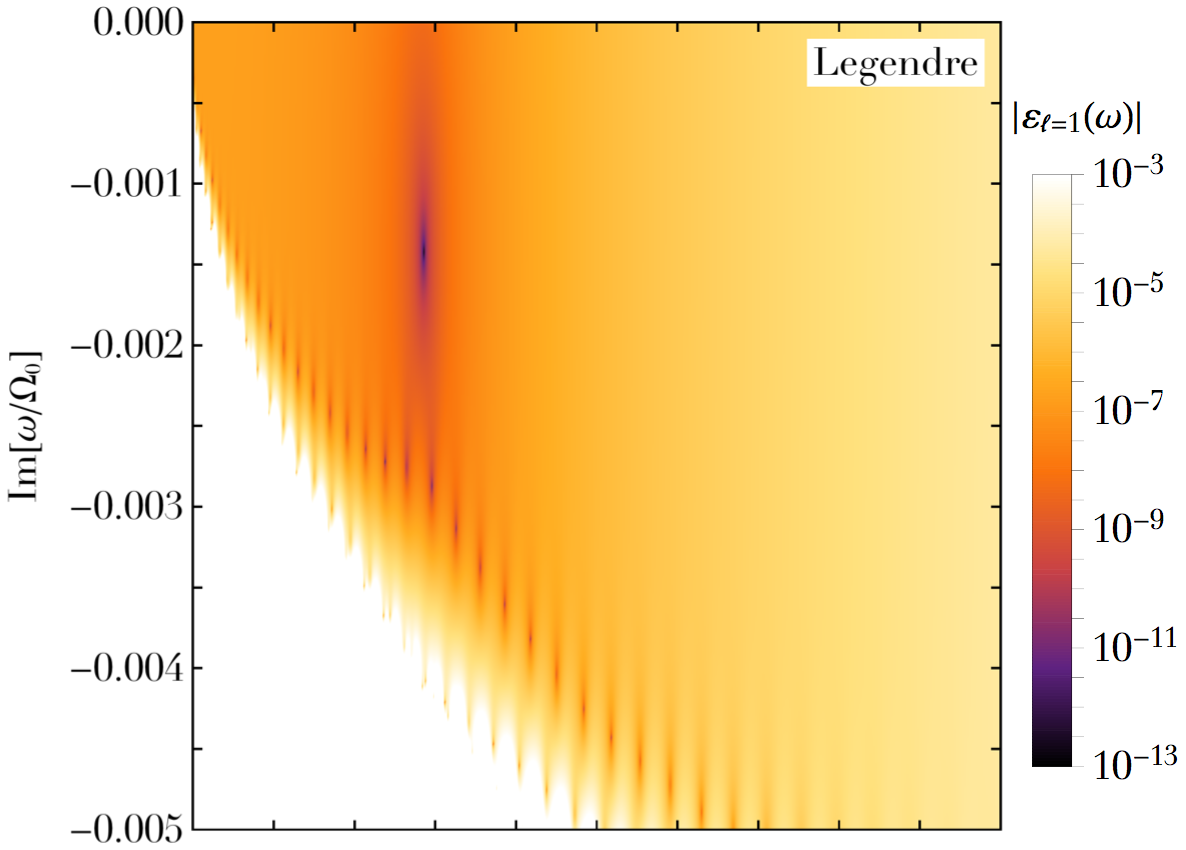
Linear response theory and damped modes of stellar clusters
We present a new method to perform explicitly Landau's prescription in stellar systems, and compute the associated response matrix.
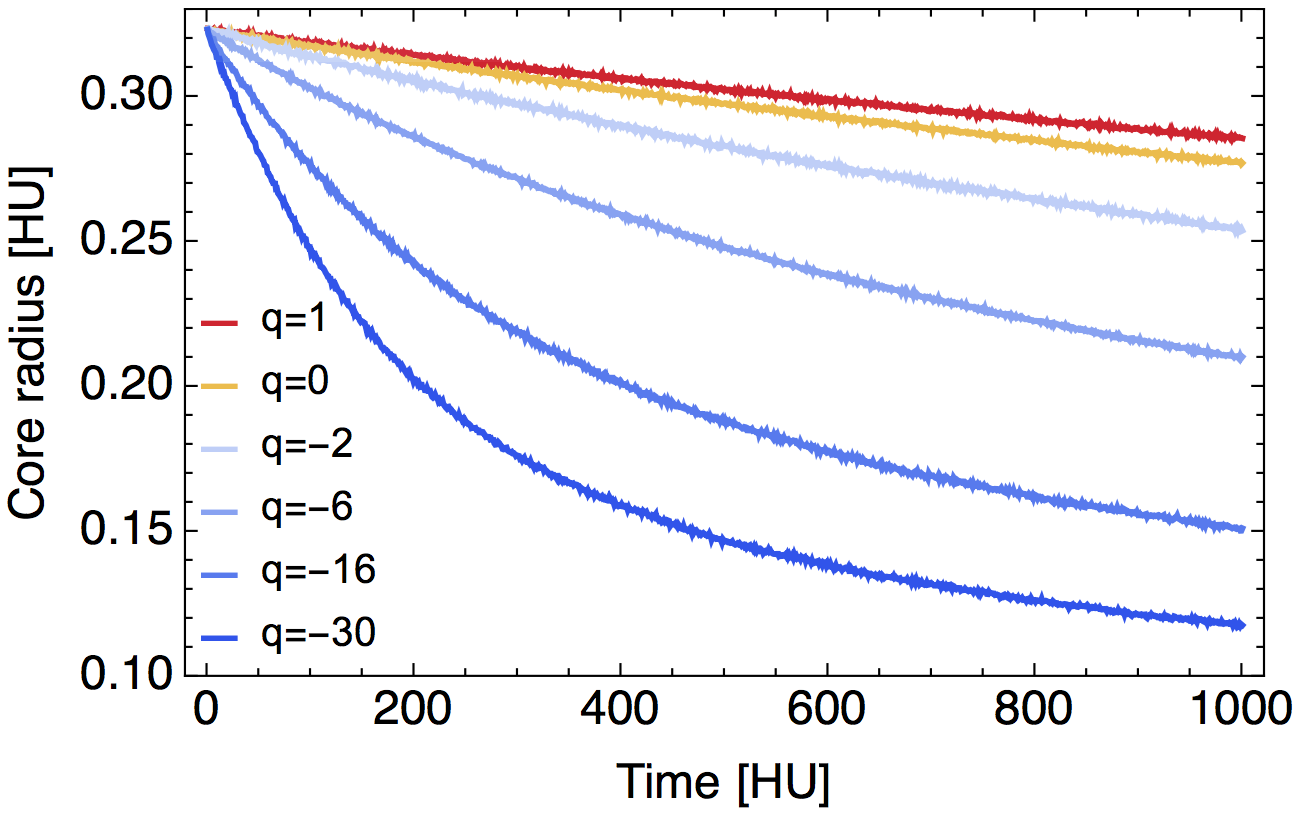
Non-resonant relaxation of anisotropic globular clusters
We consider globular clusters with anisotropic velocity distributions. We compare non-resonant kinetic theory with direct N-body measurements.

Orbital alignment and mass segregation in galactic nuclei via vector resonant relaxation
We implement a maximum entropy method to predict the thermodynamical equilibrium distribution of stellar orientations around a supermassive BH.
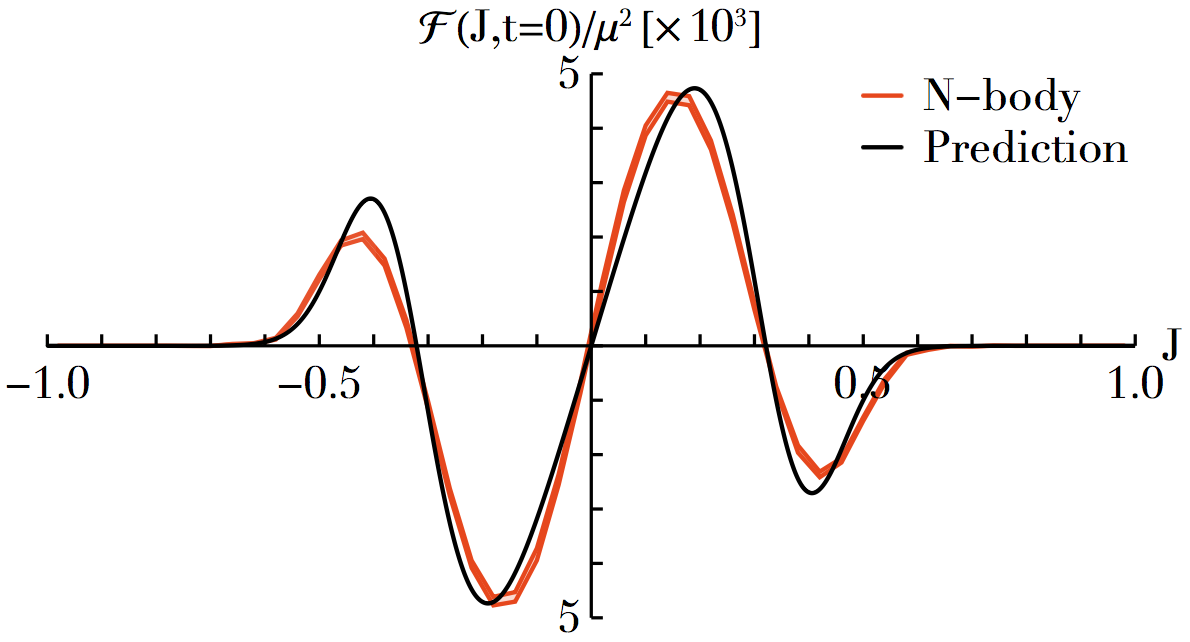
Long-term relaxation of 1D self-gravitating systems
We implement explicitly the (inhomogeneous) Balescu-Lenard equation in 1D self-gravitating systems. We perform quantitative comparisons with direct N-body measurements.
In the limit where collective effects can be neglected, we derive a closed and explicit 1/N^2 collision operator for 1D inhomogeneous systems.
Astrophysics with the Laser Interferometer Space Antenna
Review summarising the astrophysical processes relevant for the upcoming LISA interferometer.
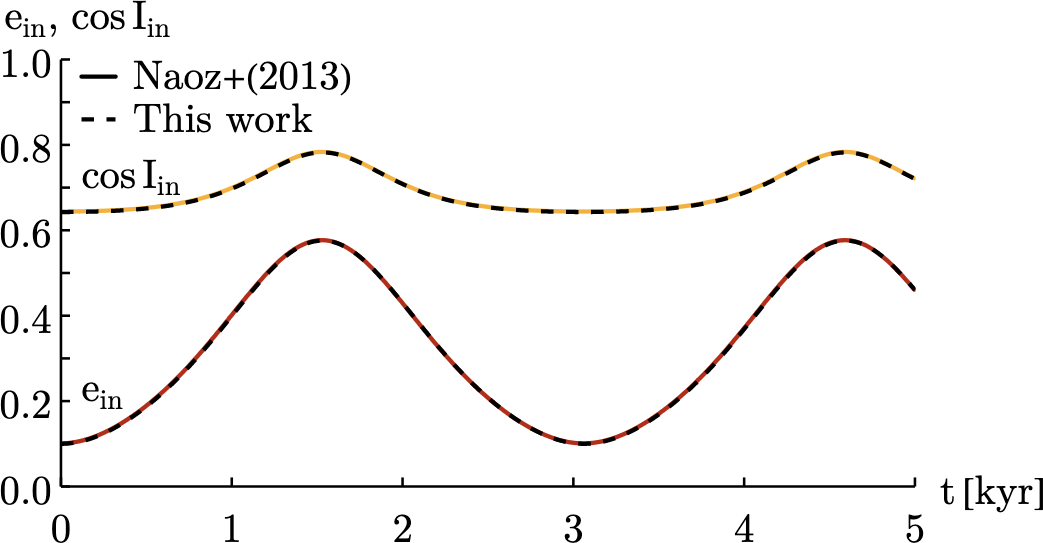
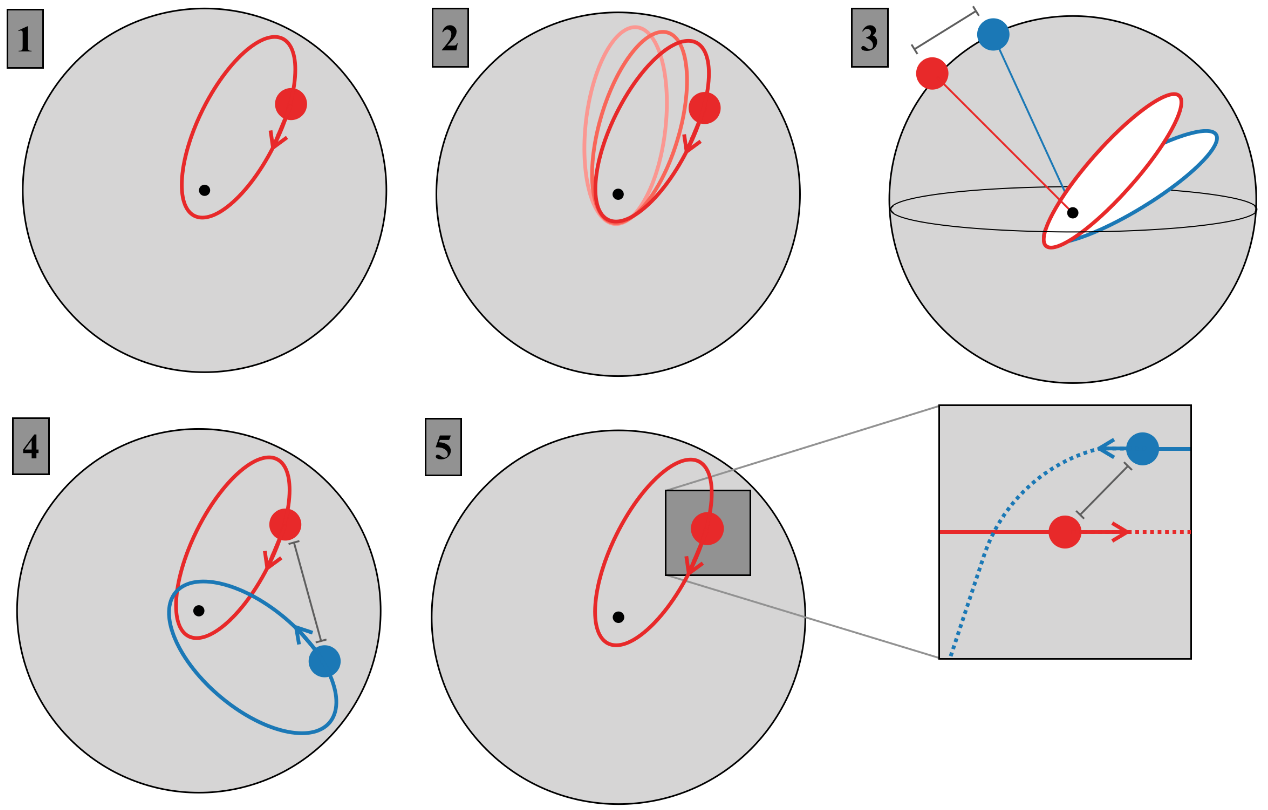
Milankovitch equations with spinors
We investigate the use of spinors to describe the secular evolution of quasi-Keplerian systems.
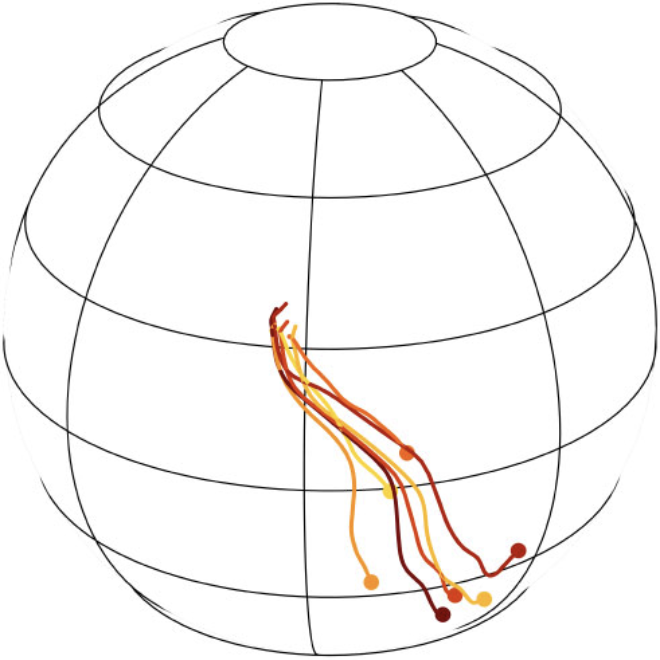
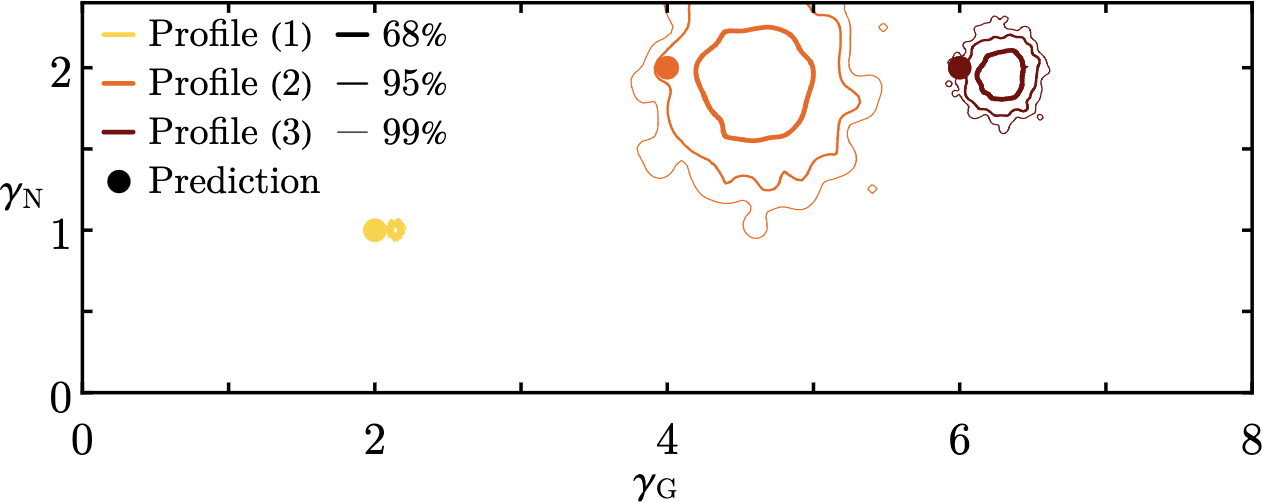
Constraining intermediate-mass black holes from the stellar disc of SgrA*
We use jointly kinetic predictions for the efficiency of dilution through vector resonant relaxation along with the recent observation of a stellar disc around SgrA*, to constrain the possible presence of intermediate mass black holes around SgrA*.
Kinetic blockings in long-range interacting systems
We investigate the long-term relaxation of systems submitted to a second-order bare kinetic blocking.
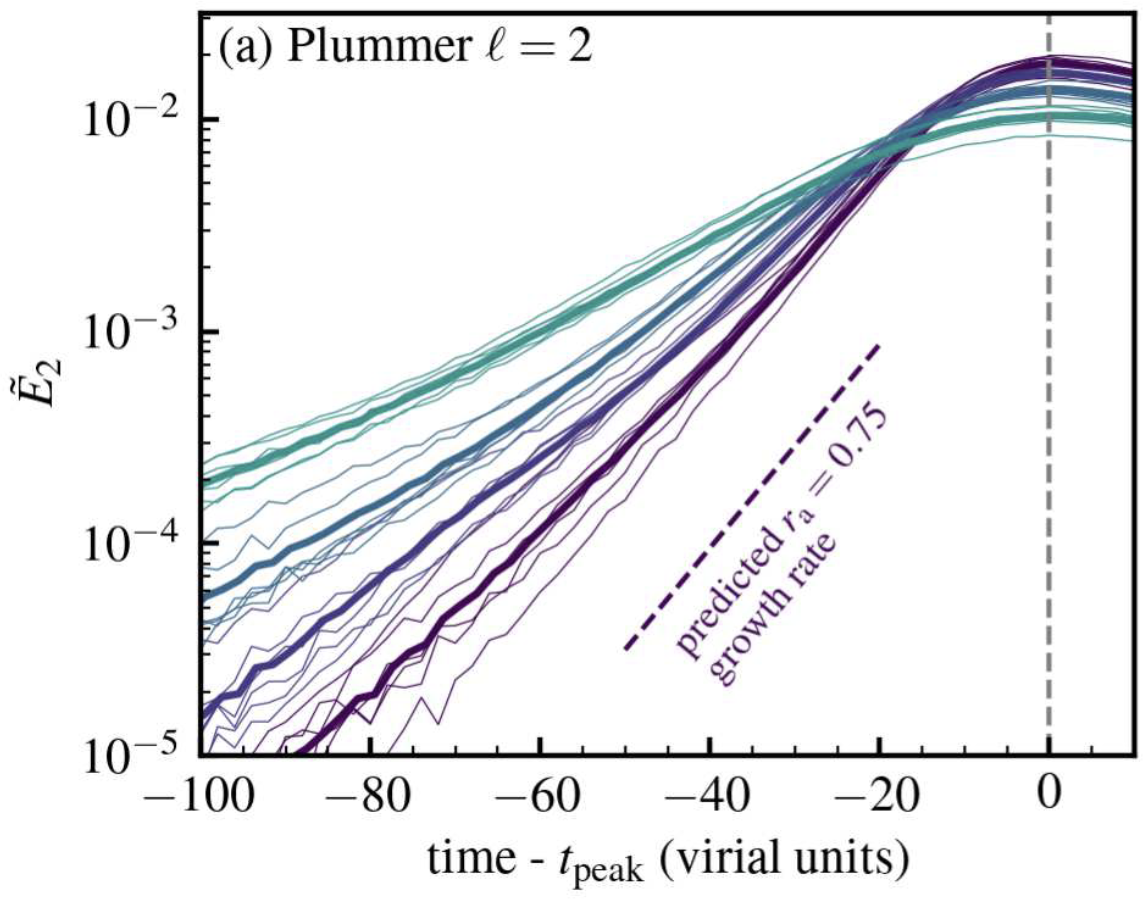
Predicting the linear response of self-gravitating stellar spheres and discs with LinearResponse.jl
We present LinearResponse.jl, an efficient, versatile public library written in julia to compute the linear response of self-gravitating stellar spheres and razor-thin discs.
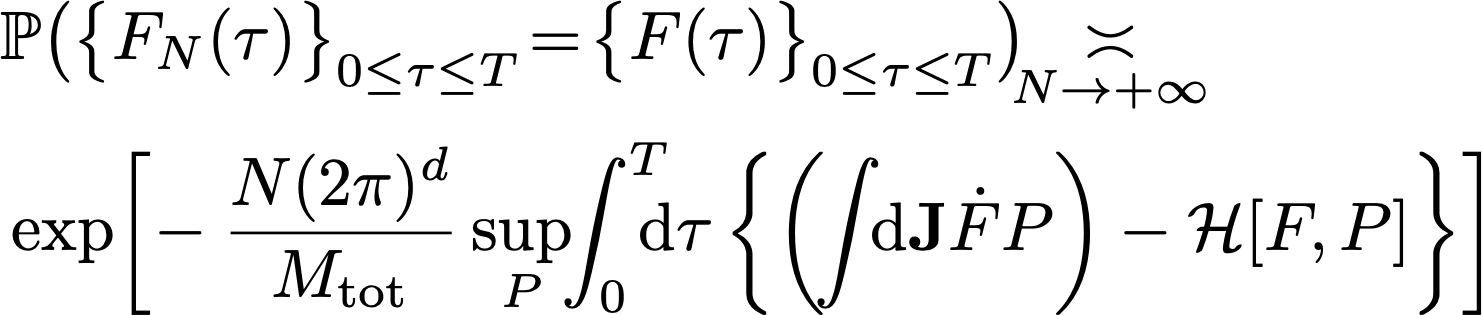
We consider the long-term evolution of an inhomogeneous long-range interacting N -body system. Placing ourselves in the dynamically hot limit, i.e. neglecting collective effects, we derive a large deviation principle for the system's empirical angle-averaged distribution function.
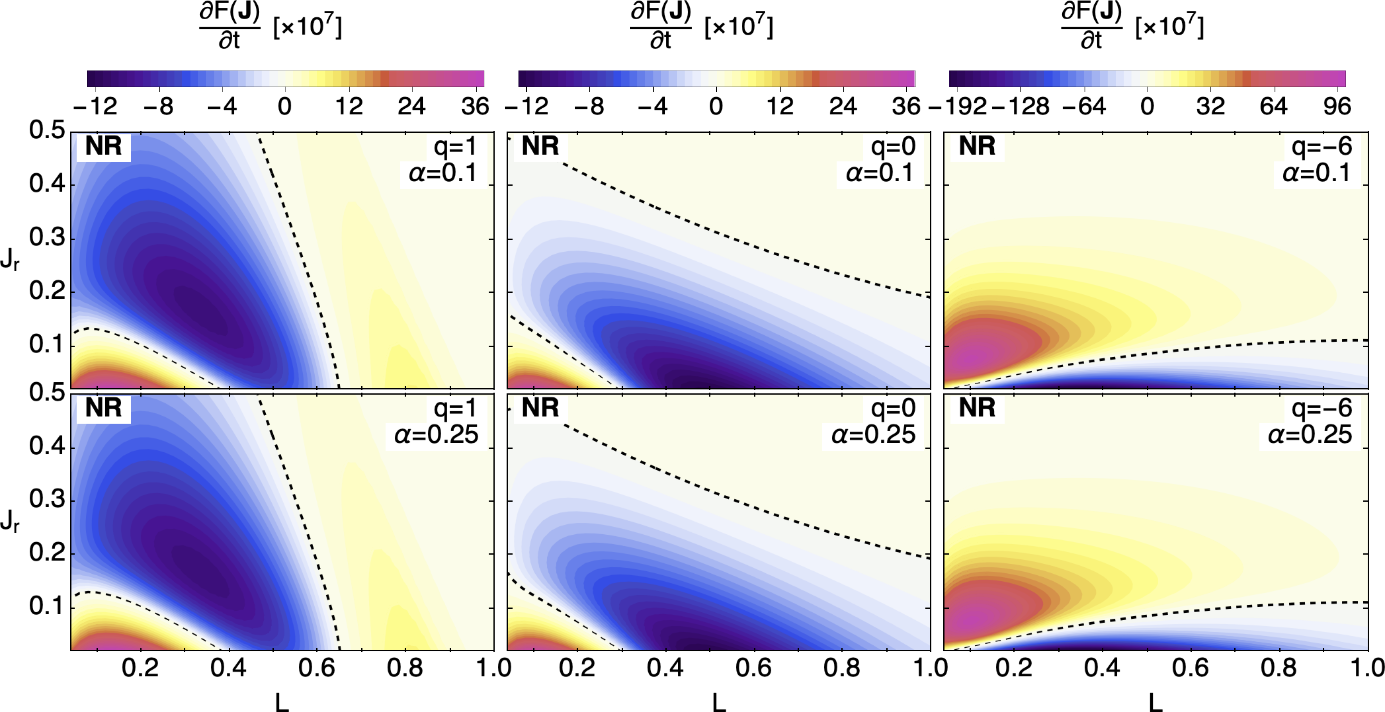
Non-resonant relaxation of rotating globular clusters
The long-term relaxation of rotating globular clusters is investigated through an extension of the orbit averaged Chandrasekhar non-resonant formalism.
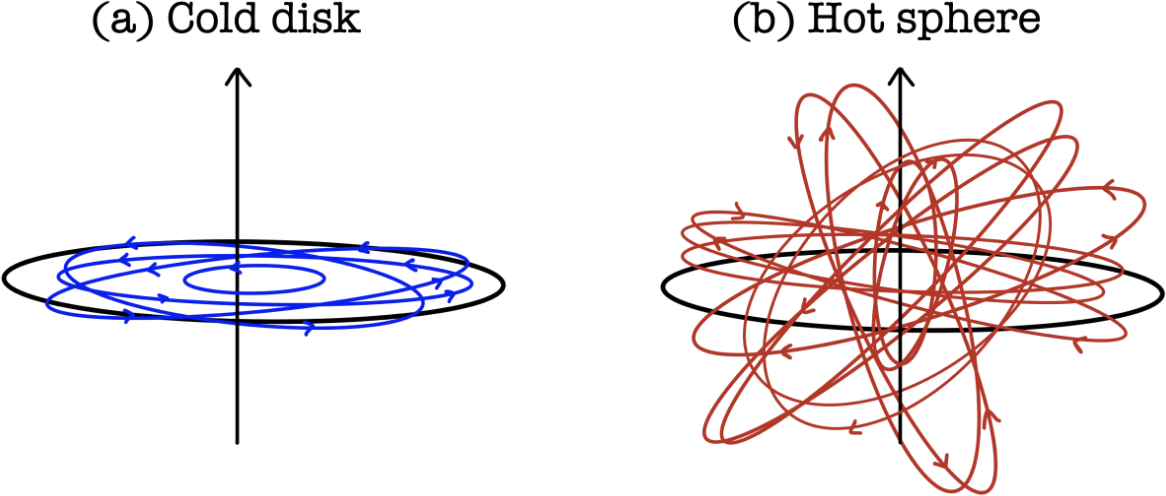
Kinetic theory of stellar systems: A tutorial
This tutorial article is an introduction to the collective dynamical evolution of the very large numbers of stars and/or other self-gravitating objects that comprise such systems, i.e. their kinetic theory.
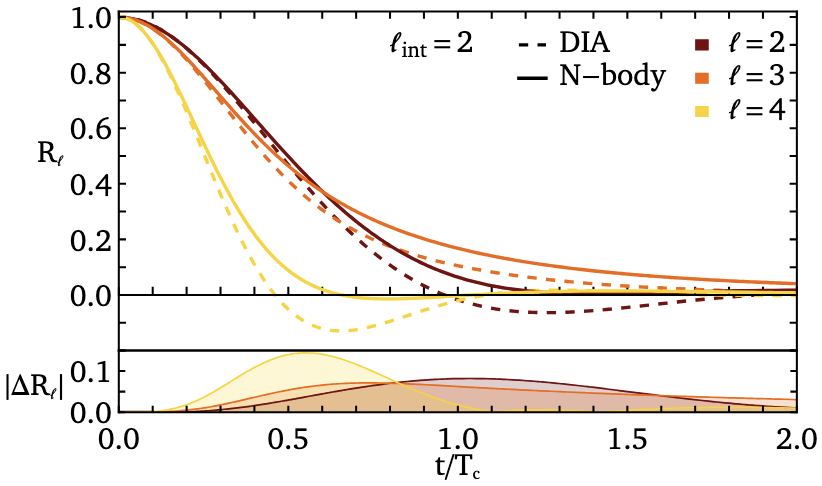
Vector resonant relation and statistical closure theory: Direct interaction approximation
We implement explicitly the Direct Interaction Approximation to predict the two-point correlation function of Vector Resonant Relaxation, i.e. the rearrangement of stellar orbital orientations around a supermassive black hole.

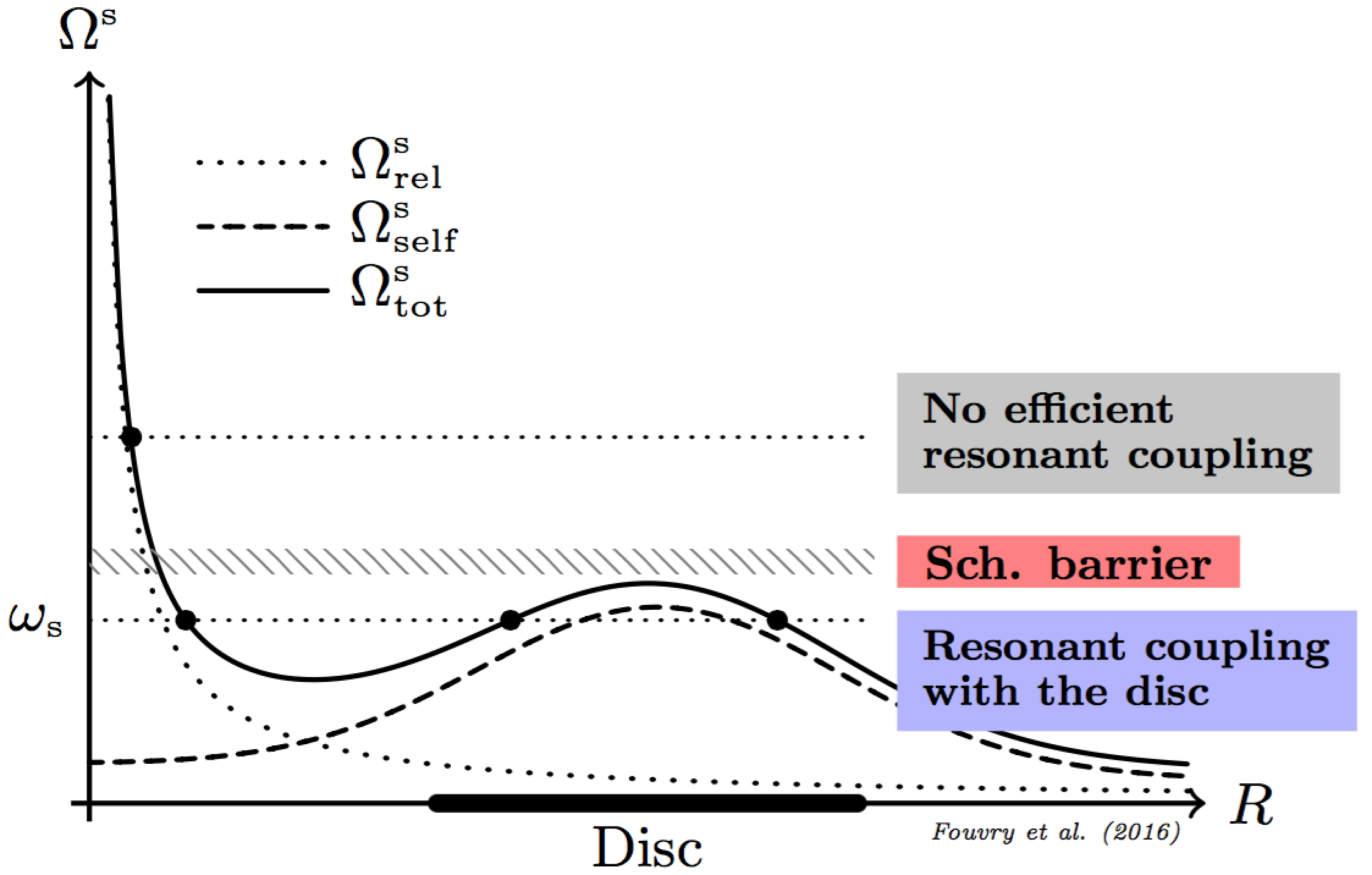
The long-term evolution of razor-thin galactic discs: Balescu-Lenard prediction and perspectives
We implement the Balescu-Lenard equation in the context of razor-thin galactic discs, highlighting in particular the crucial role played by (weakly) damped modes, and long-term stochasticity.
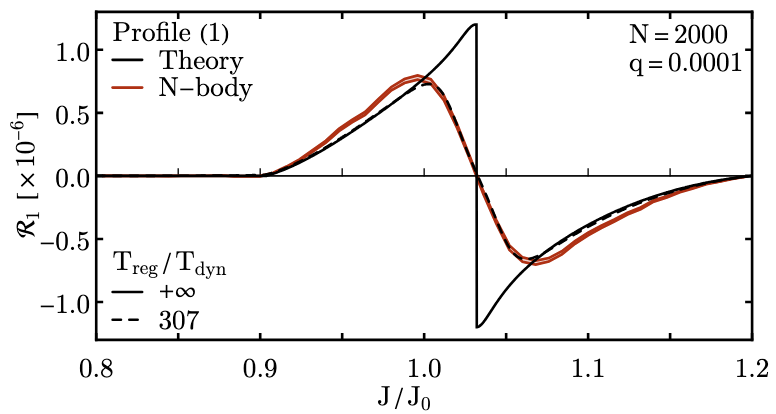
Kinetic theory of point vortices at order 1/N and 1/N^2
We investigate the long-term relaxation of a distribution of N point vortices in two-dimensional hydrodynamics, in the limit of weak collective amplification. We show the importance of resonance broadening effects, and possible kinetic blockings.