This tutorial follows the 2D discrete case example introduced in the previous section so you should probably read it first if you haven't done so yet.
We will compute the filaments and walls from the downsampled dark matter N-body simulation snapshot ${DISPERSE}/data/simu_32_id.gad. The distribution has periodic boundary conditions and we therefore start by computing its Delaunay tessellation with the following command:
The program should output a file called simu_32_id.gad.NDnet that can be used directly with mse to compute the filaments and walls of the distribution. In 3D, walls are represented by the ascending 2-manifolds that originate from critical points of critical index 1 so they can be computed with option -dumpManifolds JE1a (letter E stands for Extended, which means that the ascending 1-manifolds and ascending 0-manifolds at the boundary of the walls will also be added, see option -dumpManifolds of mse) .Note that by default, subsets of the walls that are common to several walls are merged together, so you may want to try -dumpManifolds JP1a instead if you are interested in studying the properties of individual walls. The filaments are computed with option -upSkl or -dumparcs U which are equivalent. Using interactive mode to select a persistence threshold (use -nsig 3.5 instead of -interactive if pdview could not compile on your computer), we run the following command:
which after some quick computations, should display the following persistence diagram.
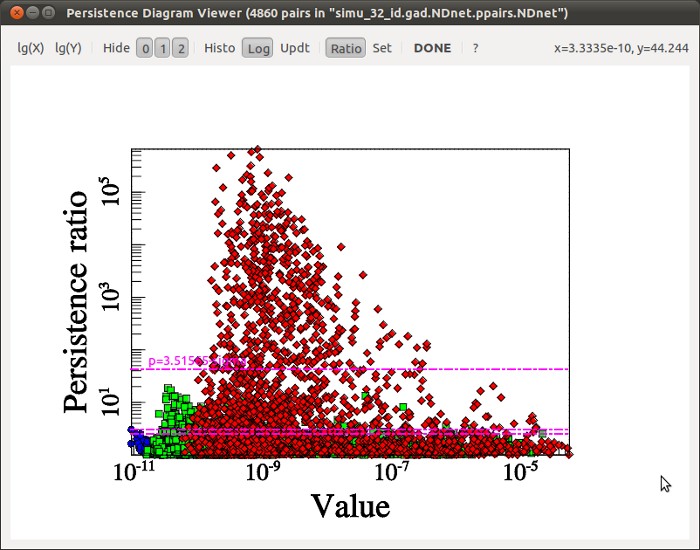
On this diagram, each type of pair is represented by a mark of different color : blue for minima/1-saddle, green for 1-saddle/2-saddle and red for 2-saddle/maxima. Note that the blue dots in the lower left corner stand for the voids in the distribution, so it is expected that we find only few of them compared to the red dots which represent collapsed structure (the simulation is 50 Mpc large). Each point on the diagram representing a topological feature, we would like to select only those points that stand out of the general distribution in terms of persistence in order to keep only the most meaningful structures (the persistence selection threshold is set by clicking while holding Ctrl key). The diagram suggests that persistence threshold should be above ~3-sigmas so we select a threshold of ~3.5 sigmas and click on the done button to confirm the selection. The program continues and should output the filaments in file simu_32_id.gad.NDnet_s3.52.up.NDskl and the walls in file simu_32_id.gad.NDnet_s3.52_manifolds_JE1a.NDnet.
It is instructive at that point to read mse output, and in particular the following section :
****** Simplifying complex ****** Starting Morse-Smale complex simplification. Computing persistence pairs ... SKIPPED. Sampling noise level was set to 3.5-sigma. Cancelling pairs with persistance ratio < [2.66e+00,3.14e+00,4.42e+01]. Tagging arcs ... done. Cancelling pairs (smart) ... (4140 rem.) done. Cancellation took 0.10s (4140 canceled, 1 conflicts, 10 loops).
what mse tells us here is that it successfully removed 4140 persistence pairs, but was not able to cancel 11 more although their persistence was lower than the threshold. The 10 loops represent persistence pairs that were connected by more than one arc at the moment of their cancellation. Topologically speaking, their cancellation is not a valid operation as it would result in a discrete gradient loop (integral lines cannot form loops in Morse-theory). Note that the existence of non-cancellable pairs is not a bug of DisPerSE but rather a feature of Morse theory. However, not cancelling them may result in a few spurious non-significant pieces of filaments remaining in the ouput file (this is very problematic though as the impact on the identified filaments is very small in general) so one can use option -forceLoops to remove them anyway (which is perfectly fine if your goal is only to identify structures). Using this option will also solve the 1 conflict identified by mse, as conflicts are the result of a non-cancellable pair blocking the cancellation of a valid cancellable pair.
We can now rerun mse while skipping the computations by loading the backup file simu_32_id.gad.NDnet.MSC that mse generated on the previous run with option -loadMSC:
and the ouput should contain the following line:
Cancellation took 0.10s (4151 canceled, 0 conflicts, 11 forced loops).
indicating that all the 4151 non persistent pairs could be cancelled.
We can now smooth and convert the resulting files to a more portable format:
skelconv simu_32_id.gad.NDnet_s3.52.up.NDskl -smooth 10 -to vtp netconv simu_32_id.gad.NDnet -to vtu netconv simu_32_id.gad.NDnet_s3.52_manifolds_JE1a.NDnet -smooth 10 -to vtu
and visualize the result with paraview. The configuration file ${DISPERSE}/data/simu_32_per.pvsm can be directly loaded in paraview (File->Load State) to make the following plot: (note that it is a bit tricky to deal with periodic boundary conditions when visualizing, clipping the boundaries is usually the easiest way)
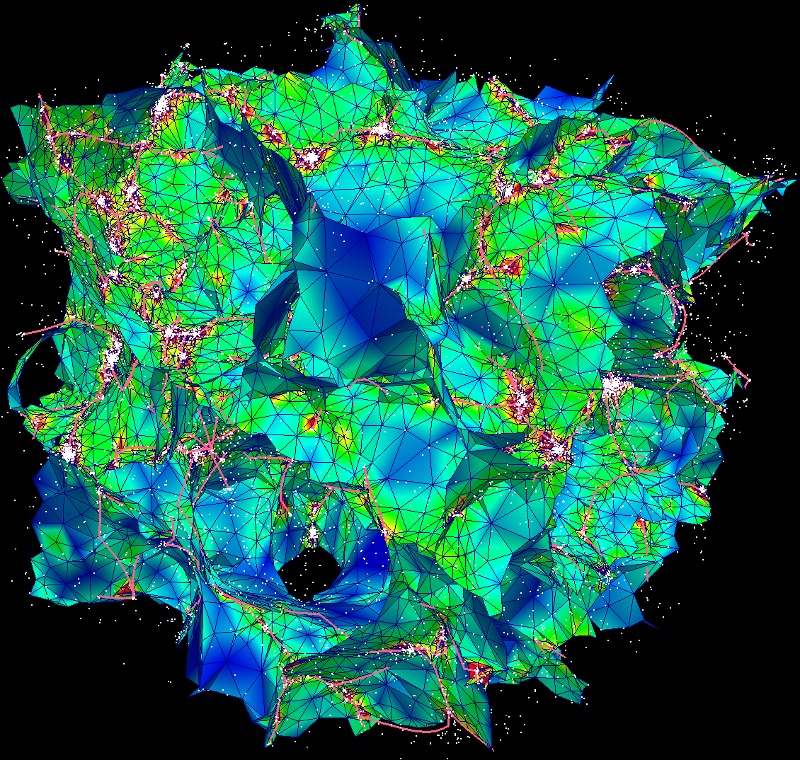
Note: contrary to the previous example where we computed 2D voids (see here), it is problematic in this case to identify each individual wall and paint it with a specific color. Indeed, contrary to voids, the 2-manifolds that represent walls can overlap, and so a unique source_index representing the critical point from which each wall originates cannot be assigned to each simplex (i.e. in that case, triangle). A solution to this problem would have been to specify that we wanted identical simplices to be stored as many times as they appear in different walls even though they are the same. This could have been achieved with flag P of option -dumpManifolds in mse:
As a result, the output file is larger, but it would also allow cross-linking the information contained in the geometry of the walls and that in the skeleton files or persistence pairs network (see this note).