Le texte ci-dessous a été rédigé suite à la requête faite par un
internaute me demandant mon sentiment sur la pertinence des travaux
effectués en cosmologie par Jean-Pierre Petit.
Il ne s'agit pas de s'attaquer à la personne Jean-Pierre Petit, mais
uniquement d'expliquer pourquoi l'intérêt de ces travaux est très
faible, comme en témoigne l'absence quasi-totale de citations de
ceux-ci dans la littérature scientifique (voir ici).
Une version plus détaillée de cette analyse sera mise en ligne
prochainement.
Je me suis procuré un des articles « fondateurs » du
modèle d'univers jumeaux de Jean-Pierre Petit (JPP), publié en 1995
dans Astrophysics and Space Science. Il y a un autre article
publié par lui à la même époque dans Il Nuovo Cimento, que je
n'ai pas encore eu sous les yeux. Il est probable que JPP ait eu
d'autres choses publiées sur le sujet, cependant l'article que j'ai
sous les yeux me paraît largement suffisant pour pouvoir émettre des
commentaires d'ordre général dont les conclusions sont résumées à la
fin de ce message.
Le modèle de JPP repose sur l'idée (probablement justifiée dans
l'autre article mentionné) que nous vivons dans un univers à courbure positive, c'est-à-dire qui est
une sorte
d'équivalent de la sphère que nous connaissons, mais avec une
dimension de plus (difficilement représentable, donc). Comme sur une
sphère ordinaire, l'on revient à son point de départ si l'on va en
« ligne droite » (si l'on suit une géodésique, devrait-on plutôt dire, mais peu
importe), et à tout point l'on peut associer un point antipodal,
c'est-à-dire le point le plus éloigné de celui où l'on se
trouve. L'idée de JPP est semble-t-il de supposer qu'il existe deux
formes de matière dans l'univers, la matière ordinaire et la matière
« gémellaire », qui possède la propriété exotique d'exercer
une gravitation répulsive sur la matière ordinaire (un peu comme deux
charges électriques de même signe qui se repoussent). Ces deux formes
de matière peuvent coexister, et ne subissent que l'influence
gravitationnelle l'une de l'autre. En fait, et c'est sans doute la
raison de supposer que la courbure est positive, on ne sent pas
l'influence de la matière gémellaire située au point où nous nous
trouvons, mais celle de la matière se trouvant au point
antipodal. Encore une fois, je ne sais pas quelle justification l'on
peut apporter à ce genre d'affirmation.
JPP suppose ensuite que l'univers est homogène et isotrope, et
qu'il y a autant de matière gémellaire que de matière ordinaire (ou
que la matière gémellaire s'identifie à la portion de matière
ordinaire du point antipodal ; ce n'est pas 100% clair, mais cela
ne change rien au problème). Résultat des courses, la densité
effective du milieu étant égale (d'après JPP) à la densité de la
matière ordinaire moins celle de la matière gémellaire, elle est nulle
(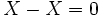 , donc). La motivation de tout cela semble résider
dans le souhait de JPP de produire facilement la répartition de la
matière dans l'univers, qui a une structure quelque peu
« spongieuse », avec des bulles relativement vides, à
l'intersection desquelle on a des surdensités (la surface des bulles),
aux intersections desquelles on a des filaments de matière nettement
plus marqués, les grosses structures (super amas) étant (schématiquement !) aux
intersections des filaments.
, donc). La motivation de tout cela semble résider
dans le souhait de JPP de produire facilement la répartition de la
matière dans l'univers, qui a une structure quelque peu
« spongieuse », avec des bulles relativement vides, à
l'intersection desquelle on a des surdensités (la surface des bulles),
aux intersections desquelles on a des filaments de matière nettement
plus marqués, les grosses structures (super amas) étant (schématiquement !) aux
intersections des filaments.
Il y a là un premier problème, que l'on pardonnera à JPP : les
simulations numériques, considérablement plus évoluées qu'il y a dix
ans (date de l'article en question), permettent de reproduire les
observations de cette répartition spongieuse de la matière dans
l'univers. J'ignore quel était l'état de l'art à l'époque, mais je
veux bien croire qu'à l'époque on ne savait faire et que JPP ait
souhaité proposer un truc radicalement nouveau pour voir si cela
pouvait expliquer plus simplement cette répartition qui d'après ses
dires restait un problème ouvert à l'époque. Car le fait est que JPP
affirme que son modèle (qui ne correspond par forcément à ce que je
viens de décrire, mais peu importe, cf plus bas) permet d'expliquer
cette répartition spongieuse. J'avoue ne pas suivre son
raisonnement. Apparemment il affirme que selon laquelle de la matière
ordinaire ou de la matière gémellaire domine localement, l'un doit
former des grumeaux, l'autre des bulles. En pratique, ces deux
configurations sont assez éloignées de ce que l'on observe, même
qualitativement (les grumeaux forment un réseau semble-t-il assez
régulier, les bulles ne forment pas vraiment d'amas aux points
d'intersection).
Là où les choses se compliquent sérieusement c'est quand par
exemple JPP affirme que son mécanisme cité plus haut (que je ne
prétends pas avoir compris dans le détail, mais peu importe, je
regarde surtout les calculs qui vont suivre) permet de se passer de
l'inflation cosmique puisqu'il permet
d'homogénéiser l'univers. Le problème c'est que cette affirmation se
base sur des hypothèses très fortes sur la répartition
« initiale » de la matière (qu'il suppose poissonienne,
c'est-à-dire explicitement homogène à grande échelle). Si l'on suppose
que l'on a des contrastes de densité importants sur des échelles
supérieures au rayon de Hubble actuel, son truc ne marche
pas du tout par exemple car l'homogénéisation ne peut se faire en un
temps égal à l'âge de l'univers (quasiment par définition). Je trouve
donc JPP soit assez filou de ne pas mentionner cela, soit
extraordinairement naïf de croire que ses conditions initiales sont
suffisamment génériques pour pouvoir être pertinentes pour résoudre le
problème qu'il prétend résoudre (l'homogénéisation de
l'univers). Rappelons qu'une des grandes forces de l'inflation est
d'homogénéiser d'immenses régions de l'univers quelles que
soient les conditions initiales (ou peu s'en faut) sur la
répartition de matière au sortir de l'époque de Planck.
Après diverses digressions assez peu intéressantes, JPP s'attaque à
des choses quantitatives : il résoud les équations de Friedmann pour son
modèle. Il remarque (fort justement) que la densité effective de
matière étant nulle, la seule solution autre que l'espace de Minkowski correspond à un facteur d'échelle qui croît linéairement
avec le temps. Dans un tel modèle, JPP fait (justement) remarquer que
la courbure spatiale est négative (c'est
écrit noir sur blanc dans le texte). JPP a-t-il seulement remarqué que
cela contredisait son hypothèse de départ (où elle est
positive) ? Si oui, il est malhonnête, si non, il ne se rend pas
compte que son modèle s'exclut de lui-même de façon assez
irrémédiable, puisqu'un espace à courbure spatiale négative est
infini, et qu'on n'a plus de relation entre un point et son image
antipodale à laquelle il tient tant. D'une certaine façon, il suffit
de remarquer cela pour ne pas à avoir lire la suite, tout en
s'interrogeant tout de même sur l'extrême faiblesse du raisonnement
proposé (le fait que la courbure spatiale est positive implique une
denstité totale strictement positive, on sait cela depuis 1917, alors
que de facto il est ici fait l'hypothèse qu'elle est nulle...).
Le second problème auquel s'attèle ensuite JPP, est de
sauver les apparences, car la loi d'expansion trouvée ne correspond
pas à ce qui est attendu (en 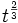 , voir ici). Là, il fait un ensemble de
manipulations bizarres et affreusement mal décrites pour expliquer que
en fait, le temps ainsi mesuré n'est pas le vrai temps indiqué par une
horloge en raison d'une hypothétique « variation des constantes
fondamentales », dont la seule raison d'être est de sauver un
modèle qui est de toute façon complètement bancal. Ce passage fait
beaucoup penser à de l'analyse dimensionnelle de base,
quoique, chose curieuse de la part de quelqu'un qui a travaillé en mécanique des fluides, le terme
d'analyse dimensionnelle ne me paraît pas être mentionné dans cet
article.
, voir ici). Là, il fait un ensemble de
manipulations bizarres et affreusement mal décrites pour expliquer que
en fait, le temps ainsi mesuré n'est pas le vrai temps indiqué par une
horloge en raison d'une hypothétique « variation des constantes
fondamentales », dont la seule raison d'être est de sauver un
modèle qui est de toute façon complètement bancal. Ce passage fait
beaucoup penser à de l'analyse dimensionnelle de base,
quoique, chose curieuse de la part de quelqu'un qui a travaillé en mécanique des fluides, le terme
d'analyse dimensionnelle ne me paraît pas être mentionné dans cet
article.
JPP réécrit donc quelques équations de la physique (équation de Schrödinger, équation de Boltzmann), et essaie de
voir comment changer les unités de longeur de temps et de masse pour
les retrouver après ces changements d'échelle. On note au passage que
l'équation de Schrödinger est mal écrite (un 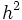 s'est glissé
en lieu et place d'un
s'est glissé
en lieu et place d'un 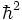 , ça fait
désordre !), et qu'en redéfinissant son étalon de longueur
, ça fait
désordre !), et qu'en redéfinissant son étalon de longueur 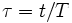 , JPP oublie qu'il suppose ensuite que son étalon
de durée, qu'il
note T varie au cours du temps, et que donc on n'a pas comme il
dit
, JPP oublie qu'il suppose ensuite que son étalon
de durée, qu'il
note T varie au cours du temps, et que donc on n'a pas comme il
dit 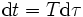 , mais
, mais 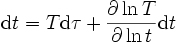 ,
qui
invalide la plupart de ses calculs. Après le coup de l'erreur
(basique) sur la courbure, il est clair qu'il n'y a plus grand chose à
espérer du modèle. Ajoutons que JPP est obligé d'ajouter à la main la
bonne variation de ses étalons d'unité pour retrouver les résultats
attendus, et que la présence avérée d'énergie noire nécessite
aujourd'hui une variation temporelle de ceux-ci extraordinairement
plus ad hoc encore pour que cela marche.
,
qui
invalide la plupart de ses calculs. Après le coup de l'erreur
(basique) sur la courbure, il est clair qu'il n'y a plus grand chose à
espérer du modèle. Ajoutons que JPP est obligé d'ajouter à la main la
bonne variation de ses étalons d'unité pour retrouver les résultats
attendus, et que la présence avérée d'énergie noire nécessite
aujourd'hui une variation temporelle de ceux-ci extraordinairement
plus ad hoc encore pour que cela marche.
Ajoutons l'absence de résultats quantitatifs testables, une non
discussion sur le comportement de ces étalons dans un régime (l'époque
de la nucléosynthèse primordiale) où
ils devraient encore changer de façon ad hoc (mais différente !)
dans son modèle pour coller aux observations, et la liste est loin
d'être complète. Par exemple, il trouve que l'entropie d'un volume
comobile n'est pas conservée, ce qui est assez curieux car d'habitude
l'identité de Bianchi et
l'homogénéité imposent qu'elle est conservée. Il apparaît en tout cas
qu'il y a une erreur quand JPP écrit les équations d'Einstein car il oublie un
facteur
c2 quelque
part, et que oublier un tel facteur quand on pond une théorie où
c (la vitesse de la lumière) varie, c'est
l'assurance que
l'on oublie un terme supplémentaire dans les équations d'Einstein (la
même erreur que João Magueijo dans sa théorie de la vitesse
de la
lumière variable, qui est fausse de A à Z à cause de cela)...
Pour conclure :
- Plusieurs erreurs de base
(incohérence sur la signe de la courbure spatiale, mauvaise définition
du tenseur énergie impulsion) qui disqualifient irrémédiablement le
modèle.
- Méconnaissance ou incompréhension de notions de cosmologie (problème de l'horizon, notamment).
- Nombreuses
erreurs de frappe et de calcul (équation de Schrödinger, non prise en
compte de la variation temporelle de l'étalon de durée).
- Hypothèses ad hoc (forme de la variation des étalons de durée)
pour sauver un modèle qui ne semble de toute façon pas bien justifié
théoriquement.
- Beaucoup de points mal détaillés.
- Aucune prédiction quantitative, et par conséquent aucune
comparaison aux données actuelles. C'était pardonnable en 1995, mais
certainement plus maintenant. En cosmologie comme ailleurs en
astrophysique, on ne peut prétendre avoir le moindre sérieux si on ne
fait pas de prédictions quantitatives.
Dernière
modification le 18 décembre 2006
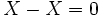 , donc). La motivation de tout cela semble résider
dans le souhait de JPP de produire facilement la répartition de la
matière dans l'univers, qui a une structure quelque peu
« spongieuse », avec des bulles relativement vides, à
l'intersection desquelle on a des surdensités (la surface des bulles),
aux intersections desquelles on a des filaments de matière nettement
plus marqués, les grosses structures (super amas) étant (schématiquement !) aux
intersections des filaments.
, donc). La motivation de tout cela semble résider
dans le souhait de JPP de produire facilement la répartition de la
matière dans l'univers, qui a une structure quelque peu
« spongieuse », avec des bulles relativement vides, à
l'intersection desquelle on a des surdensités (la surface des bulles),
aux intersections desquelles on a des filaments de matière nettement
plus marqués, les grosses structures (super amas) étant (schématiquement !) aux
intersections des filaments.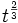 , voir
, voir 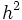 s'est glissé
en lieu et place d'un
s'est glissé
en lieu et place d'un 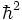 , ça fait
désordre !), et qu'en redéfinissant son étalon de longueur
, ça fait
désordre !), et qu'en redéfinissant son étalon de longueur 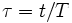 , JPP oublie qu'il suppose ensuite que son étalon
de durée, qu'il
note T varie au cours du temps, et que donc on n'a pas comme il
dit
, JPP oublie qu'il suppose ensuite que son étalon
de durée, qu'il
note T varie au cours du temps, et que donc on n'a pas comme il
dit 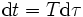 , mais
, mais 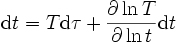 ,
qui
invalide la plupart de ses calculs. Après le coup de l'erreur
(basique) sur la courbure, il est clair qu'il n'y a plus grand chose à
espérer du modèle. Ajoutons que JPP est obligé d'ajouter à la main la
bonne variation de ses étalons d'unité pour retrouver les résultats
attendus, et que la présence avérée d'énergie noire nécessite
aujourd'hui une variation temporelle de ceux-ci extraordinairement
plus ad hoc encore pour que cela marche.
,
qui
invalide la plupart de ses calculs. Après le coup de l'erreur
(basique) sur la courbure, il est clair qu'il n'y a plus grand chose à
espérer du modèle. Ajoutons que JPP est obligé d'ajouter à la main la
bonne variation de ses étalons d'unité pour retrouver les résultats
attendus, et que la présence avérée d'énergie noire nécessite
aujourd'hui une variation temporelle de ceux-ci extraordinairement
plus ad hoc encore pour que cela marche.