Some aspects of circular prograde orbits in an extreme Kerr metric


Alain Riazuelo

  Updated 7 March 2012

Introduction

In all what follows, I shall show what an observer would see in the vicinity of an extreme (a = M) Kerr black hole. The observer is supposed to be in a circular, prograde equatorial orbit. The black hole is assumed to rotate counterclockwise with respect to the north pole, which is supposed to be seen upward.

The celestial sphere corresponds to the sky seen from Earth we are familiar with, but no stars are shown : only a pixellised version of the celestial sphere is shown here, taken from the 2MASS near infrared survey. Here, the Galactic plane does not match the black hole equatorial plane. The images are now computed at a resolution of 3600×3600 pixels.  In order to reduce the number of views and to allow seeing every direction, pictures have been computed in fish-eye format that is adapted to digital planetarium, under the so-called DomeMaster format: the disk that fits inside the images correspond to exactly 2 π steradians (i.e., a half sphere). Aberration and Doppler effect are taken into account, although imperfectly for the latter, since only a bolometric correction is applied to pixel intensity (intensity changes, but not hue). I show below and comment the view for decreasing values of the orbital radius r, which can be as small as M. Numerical stability seems OK, although some small problems are visible when looking carefuly at the high resolution views.

r = 6 M

First, here are the front and rear view for an orbit at r = 6 M, which corresponds to the innermost stable circular orbit for a Schwarshild black hole. The general aspect of the black hole silhouette differs here from that of a Schwarzschild black hole since it is not circular but shows a "D" shape as was first shown by Bardeen in the early 70's. The rounded part of the silhouette is delineated by photons which had a retrograde orbit close to the black hole, where as the straight part is delineated by photons with a prograde orbit. The latter get closer to the black hole than the former, hence the different shape for both side. Note that in addition to being asymetric, the silhouette appears to be elongated rather than flattened along the polar axis.

The primary image of the Milky Way is easy to spot on both views. On the left image, it is seen below the black hole. Around the black hole, one also sees several ghost images of the Milky Way (click on the image to enlarge it). A specificity that will become more obvious later (i.e., closer to the black hole) is that the ghost images have a much larger angular size on the prograde photon side.

r = 6 M, rear view r = 6 M, front view
Click on the images to enlarge

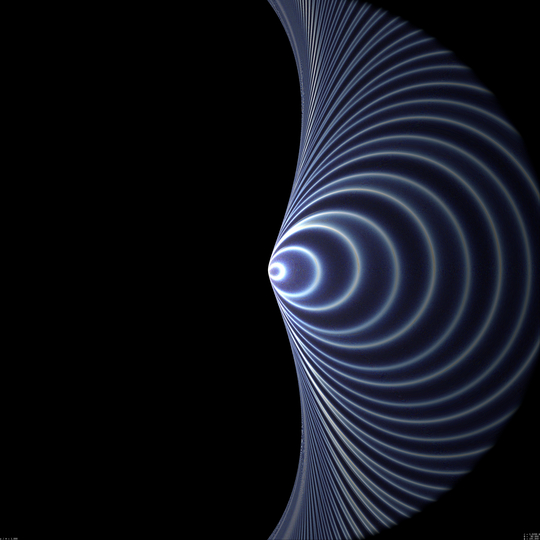
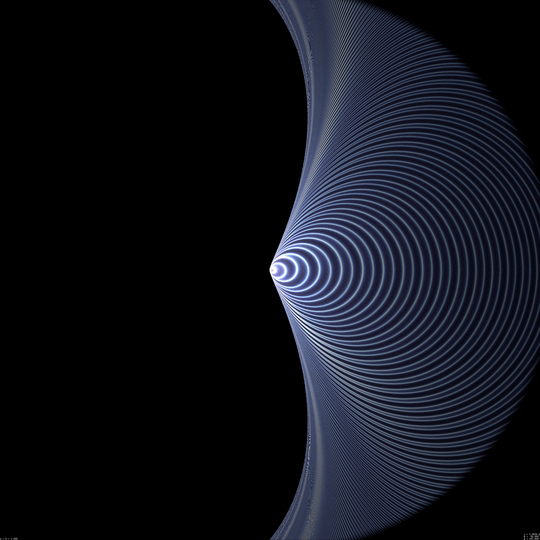
r = 3 M

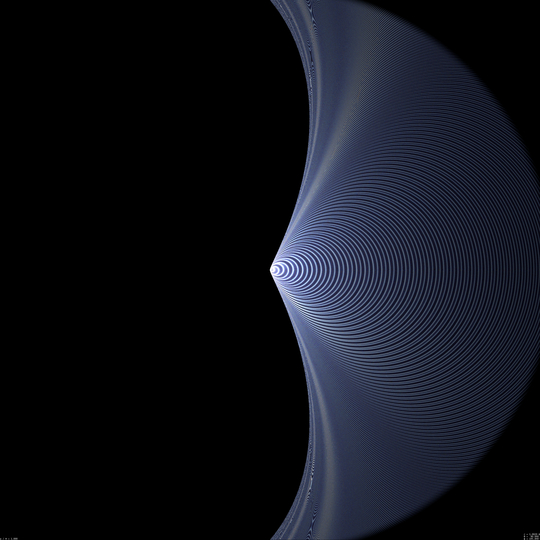
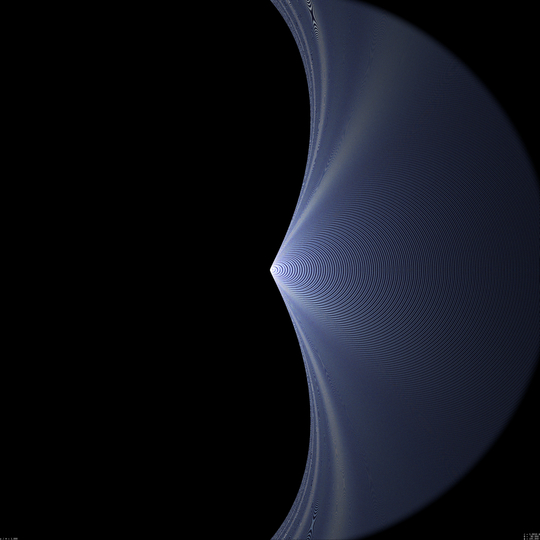
This value correspond to innermost unstable null-like circular orbits in the Schwarzschild metric. However it has nothing special in the Kerr case. When getting closer to the black hole, its angular size increases, which makes it difficult to see both edges of its silhouette, even on a hemispherical image. I shall therefore compute two separate images, one showing the front direction of the observer, where he/she sees blueshifted photons along retrograde orbits, the other showing the rear direction, where the observer is caught by photons which, like him/her, travel along prograde orbits. This "prograde" (i.e., redshifted) view will be shown on the left in what follows, whereas "retrograde" (i.e., blueshifted) view will be shown on the right. Note that when r will become smaller than 2 M, i.e. when the observer is in the ergosphere, I do not really understand whether the concept of "looking in the direction where one travels" has a meaning. Nevertheless, the "front" and "rear" directions can be, at least approximatively, guessed from te variation in redshift of the direction one is looking at.


r = 3 M, rear view r = 3 M, front view
Click on the images to enlarge

r = 1.5 M

As one enters in the ergosphere, the aspect of the black hole silhouette significantly changes (but I do not know whether the two are related). It is no longer convex, but rather concave, both in the prograde and in the retrograde direction. In the prograde direction, the number of ghost images begins to become large, even at this rather moderate resolution (8' per pixel). Note also that on the retrograde side, the primary image of the Milky Way has significantly changed. I do not know whether it primarily comes from the fact that one is nearer to the black hole or from the fact that one does not sit along the "same" azimuthal angle  (the observer is  at the same value of the Boyer Lindquist φ angle regardless of the value of r, but maybe this is not the most appropriate choice).

r = 1.5 M, rear view r = 1.5 M, front view
Click on the images to enlarge

Going deeper in the ergosphere


In what follows, the observer orbital radius is 1.2 M, 1.1 M, 1.05 M, 1.02 M, 1.01 M, 1.005 M, 1.002 M, 1.001 M, 1.0005 M, 1.0002 M and 1.0001 M, respectively. The thickness of the celestial sphere ghost images increases as r decreases. the view at r =1.01 M is quite aesthetic. On the prograde view, some bubble-like structures are easier and easier to spot as r decreases. These are definitely unphysical moiré-like pattern due to an insufficient resolution of the images. When seen at higher resolution, these structures disappear, but actually reappear closer to the black hole silhouette since they are also due to the fact that the image resolution is again insufficient as one looks closer and closer to the edge of the black hole. Note that for small r (1.005 M, say) you need to click on the picture to enlarge it in order to see the full scope of multiple images. However, even at full 3600×3600 resolution, the smaller r image not longer manages to see all of them. Visualizing the full richness of the image necessitates an increasing resolution as r decreases!

r = 1.2 M, rear view r = 1.2 M, front view
r = 1.2 M; Click on the images to enlarge


r = 1.1 M, rear view r = 1.1 M, front view
r = 1.1 M; Click on the images to enlarge


r = 1.05 M, rear view r = 1.05 M, front view
r = 1.05 M; Click on the images to enlarge


r = 1.02 M, rear view r = 1.02 M, front view
r = 1.02 M; Click on the images to enlarge


r = 1.01 M, rear view r = 1.01 M, front view
r = 1.01 M; Click on the images to enlarge


r = 1.005 M, rear view r = 1.005 M, front view
r = 1.005 M; Click on the images to enlarge


r = 1.002 M, rear view r = 1.002 M, front view
r = 1.002 M; Click on the images to enlarge


r = 1.001 M, rear view r = 1.001 M, front view
r = 1.001 M; Click on the images to enlarge


r = 1.0005 M, rear view r = 1.0005 M, front view
r = 1.0005 M; Click on the images to enlarge


r = 1.0002 M, rear view r = 1.0002 M, front view
r = 1.0002 M; Click on the images to enlarge


r = 1.0001 M, rear view r = 1.0001 M, front view
r = 1.0001 M; Click on the images to enlarge

What happens below r = 1.0001 M?

At the moment of writing, my code experiences a series of problems for r < 1.0001 M in addition to becoming extremely slow. I presume that the number of ghost images of significant angular size will be ever increasing as the orbit gets closer and closer to the black hole, however, I have not yet been able to check this.

Videos


For the 7 first values of r shown above, the images above are actually the first frame of 1800 frame long videos which all show a complete orbit around the black hole. Therefore, each video runs in 1 minute or 1'12", depending whether your player runs at 30 or 25 frames per second. Of course, the actual orbital period has to be scaled with the corresponding value of M one uses. An important thing to note is that when close to the black hole, the angular distance between the primary image of the Milky Way and its first ghost images is rather small (less than 10 degrees, say, for r = 1.02 M, and far less for smaller r). This means that when the observer makes one turn around the black hole, then the whole celestial sphere is moving on the right by only 10 degrees, each image of it replacing the next one! In other words, for a fixed orbital period, the angular displacement of the celestial sphere is much larger for large orbital radius than for a small one. Whether or not this is compensated by the fact that the orbital period at fixed M decreases with r is not known to me at the time of writing, however, it might happen that, contrarily to naive expectation, the view seen by an orbiting observer becomes almost still as r approaches the horizon!


r / M
 Progade view
 Retrograde view
6
 circ_6_000c_dm2q.mpg
 circ_6_000c_dm1q.mpg
3
 circ_3_000c_dm2q.mpg
 circ_3_000c_dm1q.mpg
1.5
 circ_1_500c_dm2q.mpg
 circ_1_500c_dm1q.mpg
1.2
 circ_1_200c_dm2q.mpg
 circ_1_200c_dm1q.mpg
1.1
 circ_1_100c_dm2q.mpg
 circ_1_100c_dm1q.mpg
1.05
 circ_1_050c_dm2q.mpg
 circ_1_050c_dm1q.mpg
1.02
 circ_1_020c_dm2q.mpg
 circ_1_020c_dm1q.mpg