For the sake of reproducibility of the results presented in
Fouvry, Pichon, Magorrian & Chavanis (2015), we distribute the 2D
Mathematica linear matrix reponse code which was implemented for this paper. If
ever you were to use this package, please cite our paper, where the details of the
implementation are presented.
+ A Mathematica package MatrixMethod2D.m and its notebook version MatrixMethod2D.nb . (Both have the same content.) This library allows the
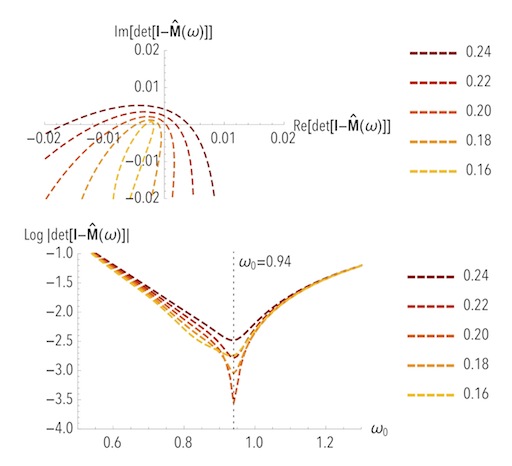
computation of the response matrix in the 2D case of an infinitely thin disc. + A Mathematica test-case notebook MestelMode.nb , which shows how the
figure C.1 from Fouvry et al. (2015) was
obtained. As the computation can be quite expensive to run, one will also find
the associated data file, Data_MestelMode.zip, which when unzipped allows not
to have to re-perform the expensive calculations needed by MestelMode.nb. In a nutshell, the library MatrixMethod2D allows for: + the determination as a function of (rp,ra) of the orbits quantities : E,
L, Jr, Ω1 and Ω2 + the construction of the 2D basis from Kalnajs (1976) + the computation of the Fourier transform of the basis elements w.r.t. the
angles + the calculation of the 2D response matrix To load the library in a Mathematica notebook, execute << "/path/to/MatrixMethod2D.m" To see all the implemented functions, execute ?MatrixMethod2D`* (Clicking on a function's name gives then more detail about its content.) An example of use of the package is given in the notebook MestelMode.nb.
This example, along with the inserted comments, should be self-explanatory on
how to proceed to the evaluation of the 2D response matrix. For any questions/remarks, please do not hesitate to contact fouvry@iap.fr