A Cosmic Ruler
(en français)
news
Results which confirm the existence of this cosmic ruler are starting
to pour in:
How can one measure the curvature of
the Universe?
A straightforward answer to this question is: "Find
a good ruler of fixed length and use it! " All that
is needed is to find a decent ruler, which can be used at large ("cosmological")
distances.
Firstly, a few words about the meaning of curvature.
If the Universe is curved, for example, a bit like the surface of the Earth
which is more or less spherical, then the relationship between the distance
to an object and the angle it subtends is not what we expect for
a flat space (a flat surface).
If someone living at the North Pole draws a map of the world on a flat
piece of paper, with herself at the centre, then she would find that the
Antarctic appears to be an enormous continent forming a ring, and that
the apparent sizes of countries in the South are all much bigger than their
real sizes. If our cartographer knows the real sizes of both the northern
and southern continents, and if she is a good mathematician, then she would
deduce from this distorted map that the surface of our planet is not flat but
spherical.
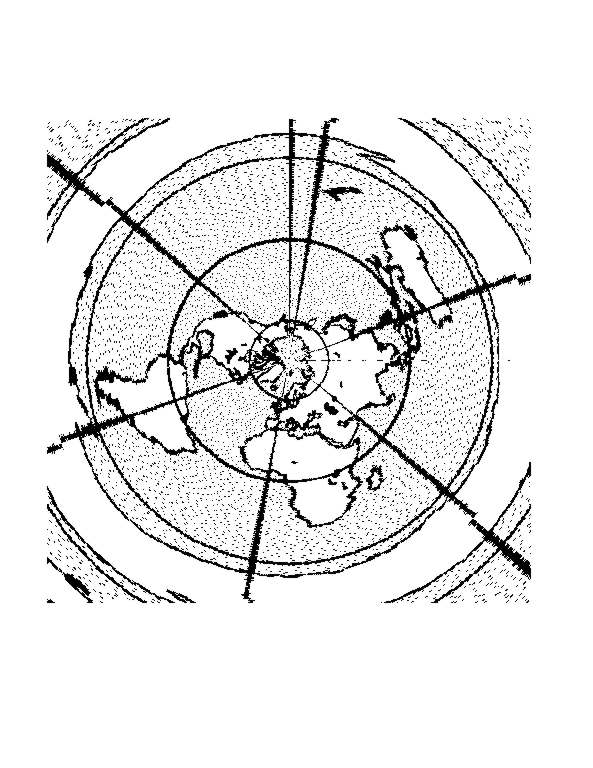
In three dimensions, astronomers attempt the same map making experiment.
If one knows in advance the real sizes of distant objects, then if their
measured angular sizes turn out to be bigger, equal or smaller than those
expected for a flat geometry, one can deduce that space is "spherical",
flat or even hyperbolic, a bit like a surface curved like a horse's
saddle.
The curvature of the Universe is a function of two parameters: firstly,
the density parameter, which is
equal to 1 if the density of the Universe is just that which
is necessary for the expansion of the Universe to slow down indefinitely
and just about stop, and secondly, the cosmological
constant, which represents and additional energy component of
the Universe, whose nature remains mysterious, which contributes to an acceleration
in the expansion of the Universe. Theoretical modelling of the Universe
when it was very young suggests that the Universe may be nearly
flat, which implies that the sum of these two
parameters should be nearly equal to 1.
To measure the curvature, it is therefore necessary to have distant
objects whose sizes are known and which can be used as cosmic
standard rulers.
Two scientists, Boud Roukema,
at IUCAA, in India (also a visitor at
DARC, Observatoire
de Paris-Meudon) and Gary
Mamon, at
IAP (also associated with the DAEC,
Observatoire
de Paris-Meudon), have recently proposed the use of the
average size of « bubbles
» of large scale structure in the Universe, traced by galaxies,
as a statistical
standard ruler for measuring the curvature of the Universe.
Indeed, on very large scales of order of many hundreds of millions of light
years, gravity has little influence on structures, so that very large
structures simply follow the general expansion of the Universe.
These structures thus serve as standard rulers in a reference frame that is
comoving with the expansion of the Universe.
In the local Universe, which is representative of the present-day Universe,
such structures formed by galaxies
are well known since the discovery in the mid 80's
of the Great Wall by Valérie
de Lapparent (IAP) and her colleagues.
All that is needed is to detect similar structures far away by using
bright enough objects, and then to find the values of the curvature parameters
for which the distant bubbles of large scale structure have, on average,
the same size as the local bubbles.
The picture below shows that the two scientists have discovered these
bubbles in the distribution of distant quasars. For these
bubbles to have the same size (the figures are compensated for the expansion of
the Universe) as the bubbles in the local Universe,
the
density parameter must be roughly 0.3, whereas the
cosmological constant is only weakly constrained. Hence, this approach
to the curvature of the Universe gives the same value of the density
parameter as the study of the speeds of galaxies in clusters and groups
of galaxies.
If this analysis is combined with those of other teams who use supernovae
(stars which explode) in distant galaxies and who deduce that the cosmological
constant is non-zero, then this shows that the
Universe is nearly flat
and that the model of an accelerating Universe (with non-zero cosmological
constant) seems to be the correct one.
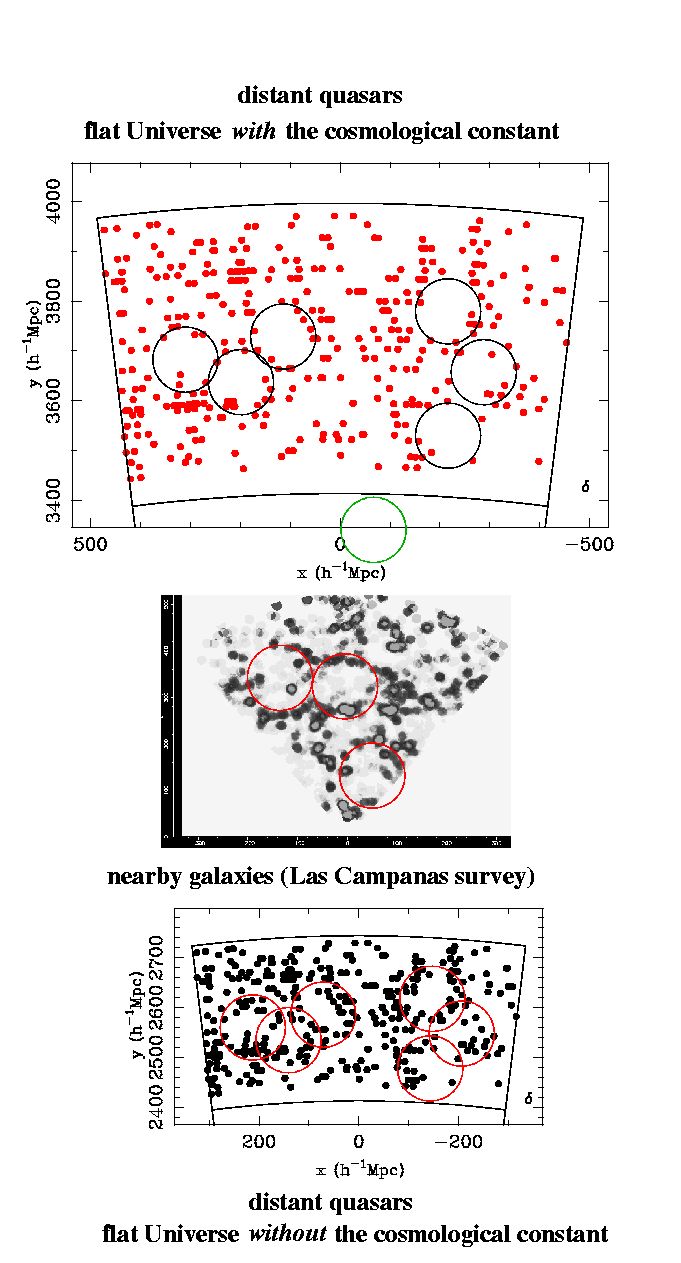
The circles drawn on the picture of the
nearby Universe (centre of the diagram, Las
Campanas survey) show in a simplified way the spatial
distribution of galaxies, in the form of bubbles and voids.
If the flat model with a cosmological
constant is correct, then it must be possible to draw circles of the same
size on the top picture (red dots,
where the curvature model is that with the density
parameter equal to 0.3 and the cosmological constant equal to 0.7)
in order to trace out the large scale structures which are far away from
us. This is indeed the case.
If the model (still fashionable very recently) of a flat universe without
a cosmological constant were the correct one, then it would be possible
to copy the circles from the nearby survey to the structures of
the survey of distant quasars shown at the bottom of the diagram
(black dots, where the density parameter equals 1
and the cosmological constant is absent). However, the circles are too big, or equivalently,
the bubbles of large scale structure are too small under this hypothesis.
In other words, it's the top picture, not the bottom one, which gives
the correct choice of the curvature parameters: the Universe is almost
flat with a non-zero cosmological constant!
In the near future, French cosmologists hope to detect the same sort
of distribution of galaxies, quasars and hot gas at great distances in
new surveys, for example, in the VIRMOS
deep survey, which is currently being carried out on a big European
optical telescope, the VLT.
With these data, we expect to deduce constraints on the curvature of the
Universe and on the cosmological constant which are even more precise than
those which we have just obtained.
Sources :
-
Research level article (difficult to read for non-specialists!):
Tangential
large scale structure as a standard ruler: curvature parameters from
quasars,
Roukema &
Mamon (2000a), Astronomy & Astrophysics 358, 395,
astro-ph/9911413
Lifting cosmic degeneracy within a single quasar survey,
Roukema &
Mamon (2000b), Astronomy & Astrophysics, in press,
astro-ph/0010511
-
quasar catalogue : Iovino,
Clowes et Shaver 1996
-
Tucker, Lin, Shectman, The
Universe on Very Large Scales: A View from the Las Campanas Redshift Survey,
in "Wide Field Surveys in Cosmology," proceedings of the 14th IAP Astrophysics
Colloquium, May 26-30, 1998, astro-ph/9902023,
Further reading:
Last modified:

