|
|
1981–82 : Mathématiques Supérieures au
Lycée Janson-de-Sailly (Paris).
1982–83 : Mathématiques Spéciales M' au
Lycée Louis-Le-Grand (Paris).
Admis à l'École Normale Supérieure de
St-Cloud (section Mathématiques).
1984 : Licence et Maîtrise de physique
fondamentale, à l'Université Paris VI.
1985 : Agrégation de sciences physiques,
option physique (reçu 5e).
1987 : DEA de physique théorique, à
l'Université Paris VI (mention TB). Rapports
intitulés "Spineurs en espace-temps courbe", sous
la direction de T. Damour (DARC, Observatoire de
Paris-Meudon) ; et "Étude théorique de
l'effet Sagnac dans un milieu matériel", sous la
direction de J.-Y. Vinet (Laboratoire d'Optique
Appliquée de l'ENSTA, Palaiseau).
1989 : Thèse de Doctorat de
l'Université Aix-Marseille II, intitulée
"Théorie de Kaluza-Klein et gravitation
quantique" (mention très honorable). Jury
composé de R. Coquereaux (directeur de thèse),
P. Méry, E. de Rafael, F. Scheck
(rapporteur), M. Veltman (rapporteur et président du
jury).
1983–88 : Élève-professeur à
l'École Normale Supérieure de St-Cloud.
1988–90 : Ancien Normalien Doctorant à
l'Université Aix-Marseille II.
1990–94 : Chargé de Recherche de 2e
classe au CNRS (CPT, Marseille).
1994–2017 : Chargé de Recherche de
1re classe au CNRS (CPT puis IAP depuis 2002).
• Médaille de bronze du CNRS 1992.
• "Outstanding referee" de l'American Physical Society depuis la
création de cette distinction en 2008.
• Prime d'excellence 2013–16 du CNRS.
1985–86 : Service National comme assistant et
professeur de physique des classes de Math. Sup. & Math.
Spé. à l'École des Pupilles de l'Air,
Grenoble.
1988–90 : Assistant des cours de relativité
restreinte et d'électromagnétisme en DEUG
2e année, à l'Université
Aix-Marseille II (poste d'Ancien Normalien Doctorant).
1993–99 : Cours de relativité
générale donnés au DEA de physique
théorique de Marseille, en collaboration avec Thomas
Schücker, et direction de plusieurs stages de DEA. Cours
d'introduction à la relativité donné en 1998
à l'école d'ingénieurs ESIM, Marseille.
Octobre 2006 : Cours avancé "Gravitation:
Theories and Experiments" donné en octobre 2006 au
Centre Émile Borel (IHP, Paris) dans le cadre du trimestre
de relativité générale.
2002–15 (inclus) : Cours de relativité
générale (15h) donnés en deuxième
année de l'École Doctorale d'Astrophysique
d'Île de France. Direction de stages, d'une thèse de
laurea italienne en 2001–02, et d'une thèse de doctorat
française en 2004–07.
2015–17 (inclus) : Cours de relativité
générale (16h + examen) donné au
Master 1 ICFP (Centre International de Physique
Fondamentale) de l'École Normale Supérieure de
Paris.
Referee pour plusieurs revues : principalement
Phys. Rev. D et
Phys. Rev. Lett., mais aussi
Class. Quantum Grav.,
Commun. Math. Phys.,
Gen. Rel. Grav.,
Int. J. Mod. Phys. A,
J. Cosmol. Astropart. Phys.,
Living Rev. Rel., et
Phys. Lett. A. Rapporteur pour la
National Science Foundation (USA).
Membre du jury de plusieurs thèses.
Membre du Comité Local d'Organisation de plusieurs
conférences internationales, et organisateur de
plusieurs sessions parallèles de telles
conférences.
Membre du conseil scientifique de l'OSU-IAP depuis sa
création en 2007.
Membre en 2006–09 d'un projet financé par
l'ANR, consacré aux modifications de la loi de
gravitation à grande distance.
Membre et co-rédacteur en 2011–2015 du programme
ANR blanc "THALES" (Théories alternatives pour la
matière et l'énergie sombres).
Membre du GDR "Gravitation et Expérience" (GREX)
durant toute son existence en 1995–2006, et représentant
de ce GDR au Centre de Physique Théorique (Marseille)
jusqu'en 2001.
Membre du comité scientifique de la
fédération de recherche "Gravitation et physique
fondamentale dans l'espace" (GPhyS) durant toute son existence en
2009–13, et représentant du GReCO/IAP.
Membre du réseau européen "Sources of
Gravitational Radiation".
Membre des commissions de spécialistes
(29e section) des Universités de la
Méditerranée (Aix-Marseille II), de Provence
(Aix-Marseille I) et de Tours, durant plusieurs années.
Co-responsable informatique du groupe "Interactions
fondamentales" au Centre de Physique Théorique
(Marseille), jusqu'à mon départ en 2000.
1988 : Harvard University, Cambridge (USA), 2 mois.
1991 : IHÉS, Bures-sur-Yvette, 3 mois.
1991–92 : IHÉS, Bures-sur-Yvette, 1 an.
1995–96 : Brandeis University, Waltham (USA), 1 an.
1997 : IHÉS, Bures-sur-Yvette, 1 mois.
2000–2001 : DARC (Meudon) puis IAP (Paris), 2 ans.
Août 1989 : École d'été
"Physics, Geometry and Topology", Banff (Canada).
Mai 1991 : Journées Relativistes,
Cargèse.
Décembre 1991 : "Dynamics of Complex and
Irregular Systems", Bielefeld (Allemagne).
Janvier 1992 : Rencontres de Moriond, Les Arcs.
Juillet 1992 : École d'été
"Gravitation and Quantizations", Les Houches.
Février 1993 : Rencontres de Moriond,
Villars-sur-Ollon (Suisse).
Juin 1993 : "First Carribean Spring School of
Mathematics and Theoretical Physics", Saint François
(Guadeloupe).
Juillet 1993 : "International Europhysics Conference
on High Energy Physics", Marseille.
Septembre 1993 : "École de Cosmologie",
Marseille.
Juin 1994 : "Advanced topics in applied mathematics
and theoretical physics", Marseille.
Septembre 1994 : "École de Cosmologie",
Marseille.
Août 1995 : "14th International Conference on
General Relativity and Gravitation", GR14, Florence
(Italie).
Mars 1996 : "Boston Colloquium for the Philosophy of
Science: Foundations of Quantum Field Theory", Boston (USA).
Mai 1996 : "The Journal of Differential Geometry
Conference on Geometry and Topology", Harvard, Cambridge
(USA).
Septembre 1996 : "Pulsar Timing, General Relativity,
and the Internal Structure of Neutron Stars", Amsterdam
(Hollande), conférencier invité.
Mars 1997 : "Géométrie non-commutative
et interactions fondamentales", Marseille.
Septembre 1997 : "Gravitation and Experiment", Les
Houches.
Décembre 1997 : "Gravitational Radiation and
Quantum General Relativity", Golden Jubilee of the Raman Research
Institute, Bangalore, (Inde), conférencier
invité.
Décembre 1997 : "15th International Conference
on General Relativity and Gravitation", GR15, Puna
(Inde).
Octobre 1998 : Conférence du 40e
anniversaire de l'IHÉS, Bures-sur-Yvette.
Janvier 1999 : Rencontres de Moriond, Les Arcs,
conférencier invité.
Janvier 2000 : Conférence "Astroparticule",
CNRS Paris.
Juillet 2000 : 9e conférence Marcel
Grossmann, MG9, Rome (Italie).
Octobre 2001 : Journées du GDR "Gravitation et
Expérience" (GREX), Grasse.
Juillet 2002 : 18e colloque de l'IAP "On
the Nature of Dark Energy", Paris (membre du comité local
d'organisation).
Décembre 2002 : Journées
thématiques de l'Université Pierre & Marie
Curie "Gravitation sur terre et dans l'espace : projets et
enjeux", Paris.
Mars 2003 : XXXVIIIes Rencontres de
Moriond, Les Arcs.
Mai 2003 : Joint BURST 2003/5th EU Network Meeting
sur "Theory and Detection of gravitational waves", Orsay.
Juillet 2003 : 10e conférence
Marcel Grossmann, MG10, Rio de Janeiro, Brésil
(organisateur de la session parallèle PT1 "Strong Gravity
and Gravitational Waves").
Octobre 2003 : Journées du GDR "Gravitation et
Expérience" (GREX), IAP, Paris.
Juillet 2004 : Colloque "Phi in the sky: The quest
for cosmological scalar fields", Porto, Portugal,
conférencier invité.
Juillet 2004 : "17th International Conference on
General Relativity and Gravitation", GR17, Dublin
(Irlande).
Octobre 2004 : "VIIe École de
Cosmologie", Marseille, conférencier
invité.
Octobre 2004 : Journées du GDR "Gravitation et
Expérience" (GREX), Nice.
Janvier 2005 : Journées de LISA-France,
APC/Collège de France, Paris.
Janvier 2005 : Journées thématiques
"Tests de la relativité générale", CPPM,
Marseille.
Juillet 2005 : 21e colloque de l'IAP "Mass
Profiles and Shapes of Cosmological Structures", Paris.
Juillet 2005 : "Albert Einstein Century International
Conference", Unesco, Paris.
Juillet 2005 : 33rd SLAC Summer Institute on Particle
Physics, SSI 2005, "Gravity and the Quantum World in the
Cosmos", Stanford, USA, conférencier
invité.
Octobre 2005 : Journées du GDR "Gravitation et
Expérience" (GREX), Paris.
Novembre 2005 : Atelier "l'Univers primordial",
Montpellier.
Janvier 2006 : Atelier "Pulsars, théories et
observations", Paris.
Janvier 2006 : Colloque "Gravitational Waves: Sources
and Observation" (ILIAS/ENTApP/GWA), Paris.
Septembre-Décembre 2006 : Trimestre de
relativité générale au Centre Émile
Borel (Institut Henri Poincaré), Paris,
conférencier invité.
Juillet 2007 : "18th International Conference on
General Relativity and Gravitation", GRG18, Sydney,
Australie (organisateur de la session A4 "Alternative Theories of
Gravity").
Mars 2008 : ESF Exploratory Workshop on
"Astrophysical Tests of Fundamental Physics", Porto, Portugal,
conférencier invité.
Avril 2008 : Journées du GDR
Supersymétrie, Strasbourg, conférencier
invité.
Juin 2008 : "École thématique du CNRS
sur la Masse" puis "11th Capra Conference on Radiation Reaction",
Orléans, conférencier invité (et
membre du comité scientifique).
Novembre 2008 : "IXe École de
Cosmologie", Cargèse, conférencier
invité (et co-organisateur de l'École).
Novembre 2008 : "First Paris-Stockholm workshop on
consistent infrared modifications of gravity", Paris.
Juin-Juillet 2009 : "Invisible Universe", Paris
(membre du comité local d'organisation, y compris de
la seconde semaine de conférence grand public, et
organisateur des sessions parallèles sur les
théories alternatives de la gravitation).
Juillet 2009 : "12th Marcel Grossmann Meeting",
MG12, Paris (membre du comité local
d'organisation).
Juin 2011 : Journée "Relativistic MOND versus
Cold Dark Matter", IAP, Paris.
Octobre 2012 : Colloque international "From Quantum
to Cosmos 5", Q2C5, Cologne, Allemagne,
conférencier invité.
Avril 2013 : Atelier international "GRAMAP (GRAM And
Pulsars)", Paris, conférencier invité.
Mai 2013 : Atelier international "Modern aspects of
gravity and cosmology", LPT, Orsay, conférencier
invité.
Septembre 2013 : Groupe de travail international de
la "Science Working Team" de la mission LISA Pathfinder, sur les
tests de théories alternatives de la gravitation, Centre
Francois Arago d'APC, Paris.
Avril 2014 : Colloque international "The Strong
Gravity Regime of Black Holes and Neutron Stars", 558th
WE-Heraeus Seminar, Bad Honnef (Allemagne),
conférencier invité.
Novembre 2014 : Atelier international "Modern aspects
of gravity and cosmology", LPT, Orsay.
Octobre 2015 : Atelier international "2nd
mini-workshop on gravity and cosmology", IAP, Paris.
Novembre 2015 : Atelier international "Modern aspects
of gravity and cosmology", LPT, Orsay.
Août-Septembre 2016 : Conférence
internationale "GRavitational-wave Astronomy Meeting in PAris"
(GRAMPA), IAP, Paris.
Novembre 2016 : Atelier international "Modern aspects
of gravity and cosmology", LPT, Orsay.
Novembre 2016 : Atelier international "Modified
Gravity", Laboratoire de Mathématiques et de Physique
Théorique, Tours, co-organisateur.
Décembre 2016 : Conférence
internationale "Gravity and Experiment", IAP, Paris.
Mai 2017 : Atelier international "Hot topics in
Modern Cosmology" (Spontaneous Workshop XI), Cargèse,
conférencier invité.
Juin 2017 : Conférence internationale "The Era
of Gravitational-Wave Astronomy", IAP, Paris.
Novembre 2017 : Atelier international "Modern aspects
of gravity and cosmology", LPT, Orsay.
Avril 1988 : "Champs matériels en
théorie de Jordan-Thiry", CPT, Marseille.
Novembre 1988 : "Divergences en gravitation
quantique", CPT, Marseille.
Mars 1989 : [même titre], Centre de
Physique Mathématique, Montpellier.
Avril 1989 : [même titre], LAPP,
Annecy.
Avril 1989 : [même titre], DARC,
Observatoire de Paris-Meudon.
Novembre 1989 : "Géométrie des
métriques invariantes sur SU(3)", CPT,
Marseille.
Décembre 1989 : "Divergences à une
boucle en théorie des perturbations chirales",
CPT.
Mars 1990 : "Théorie des noeuds et
polynômes invariants", CPT, Marseille.
Mai 1991 : "`Superconnexions et
géométrie non-commutative au service du
Modèle Standard", Journées Relativistes,
Cargèse.
Décembre 1991 : "Tensor-multi-scalar
theories of gravitation and strong-field tests of general
relativity", Institut für Physik, Mainz University
(Allemagne).
Janvier 1992 : [même titre],
Rencontres de Moriond, Les Arcs.
Avril 1992 : [même titre], DARC,
Observatoire de Paris-Meudon.
Novembre 1992 : "Nonperturbative strong-field
effects in tensor-scalar gravity", CPT.
Novembre 1992 : [même titre], Institut
Henri Poincaré, Université Paris VI.
Février 1993 : [même titre],
Rencontres de Moriond, Villars-sur-Ollon (Suisse).
Novembre 1993 : "Is there a scalar contribution
to gravity ?", IHÉS, Bures-sur-Yvette.
Février 1994 : [même titre],
CPT, Marseille.
Août 1995 : "A field-theory approach to
post-post-Newtonian gravity", 14th International Conference
on General Relativity and Gravitation, GR14, Florence
(Italie).
Mai 1996 : "Is there a scalar contribution to
gravity ?", Brandeis U., Waltham (USA).
de Juin à Août 1996 : "Spontaneous
scalarization of neutron stars and tests of strong-field
gravity" (I) et "Binary-pulsar tests of strong-field
gravity" (II), donnés aux États Unis à
Penn State U. (I), Maryland (I), U. of North Carolina (II),
Chicago (I), St. Louis (II), Caltech (I), Stanford (I), Montana
State U. (I), et Columbia U. à New York (II).
Septembre 1996 : "Binary-pulsar tests of
strong-field gravity", conférence "Pulsar Timing,
General Relativity, and the Internal Structure of Neutron Stars",
Amsterdam (Hollande).
Mars 1997 : "Higgs potential and conformal
transformation", conférence "Géométrie
non-commutative et interactions fondamentales", Marseille.
Septembre 1997 : "Binary-pulsar tests of
strong-field gravity", conférence "Gravitation and
Experiment", Les Houches.
Décembre 1997 : "Experimental tests of
gravitational theories", conférence "Gravitational
Radiation and Quantum General Relativity", Golden Jubilee of the
Raman Research Institute, Bangalore (Inde).
Décembre 1997 : "Binary-pulsar constraints
on the PPN ratio (beta-1)/(gamma-1)", 15th International
Conference on General Relativity and Gravitation, GR15,
Puna (Inde).
Janvier 1998 : "Introduction à la
relativité restreinte et générale",
ESIM, Marseille.
Septembre 1998 : "The theoretical significance of
gravity tests", La Plata (Argentine).
Septembre 1998 : "Strong-field tests of
gravity", Buenos Aires (Argentine).
Janvier 1999 : "Gravitational-wave versus
binary-pulsar tests of strong-field gravity", Rencontres de
Moriond, Les Arcs.
Avril 2000 : "Une approche
phénoménologique de la quintessence en gravitation
tenseur-scalaire", DARC, Observatoire de Paris-Meudon.
Juillet 2000 : "A phenomenological approach to
quintessence in scalar-tensor gravity", 9e
conférence Marcel Grossmann, MG9, Rome
(Italie).
Juillet 2000 : "Tests of strong-field gravity and
gravitational radiation damping in binary-pulsar systems",
9e conférence Marcel Grossmann, MG9,
Rome (Italie).
Octobre 2001 : "Comment l'expansion
accélérée de l'Univers contraint les
théories tenseur-scalaire", Journées du GREX,
Grasse.
Octobre 2002 : "Quintessence, scalar-tensor
gravity, and scalar-Gauss-Bonnet interaction", LPTHE,
Université Pierre & Marie Curie, Paris.
Décembre 2002 : "Cosmologie et gravitation
relativistes", journées thématiques de
l'Université Pierre & Marie Curie "Gravitation sur
terre et dans l'espace : projets et enjeux", Paris.
Décembre 2002 : "Quintessence,
scalar-tensor gravity, and scalar-Gauss-Bonnet interaction",
SPhT, Saclay.
Mars 2003 : "Scalar-tensor theories and
cosmology", XXXVIIIes Rencontres de Moriond, Les
Arcs.
Juillet 2003 : (I) "Binary-pulsar tests of
strong-field gravity and gravitational radiation damping",
(II) "Constraints on a quintessence-Gauss-Bonnet
coupling", et (III) "Reaction of a neutron
star-white dwarf binary to gravitational wave emission",
10e conférence Marcel Grossmann, MG10,
Rio de Janeiro, Brésil.
Octobre 2003 : "Binary-pulsar tests of
strong-field gravity", IAP, Paris.
Juillet 2004 : conférence
plénière "Tests of scalar-tensor gravity",
colloque "Phi in the sky: The quest for cosmological scalar
fields", Porto, Portugal.
Juillet 2004 : "Dynamics and gravitational
radiation of compact binaries completed at the third
post-Newtonian order", 17th International Conference on
General Relativity and Gravitation, GR17, Dublin
(Irlande).
Octobre 2004 : "Non-linear effects in
scalar-tensor gravity", VIIe école de
cosmologie, Marseille.
Octobre 2004 : "Recent binary-pulsar tests of
gravity and comparison with other experiments",
journées du GREX, Nice.
Janvier 2005 : "Using LISA to test General
Relativity?", journées de LISA-France,
APC/Collège de France, Paris.
Janvier 2005 : exposé grand public "Tests
de la Relativité Générale", puis
séminaire spécialisé "Tests of General
Relativity (and their theoretical significance)", CPPM,
Marseille.
Juillet 2005 : "Strong-field tests of
relativistic gravity with binary pulsars", Albert Einstein
Century International Conference, Paris.
Juillet 2005 :
"Tests
of Alternative Theories of Gravity", 33rd SLAC Summer
Institute "Gravity and the Quantum World in the Cosmos",
Stanford, USA.
Septembre 2005 : exposé grand public
"General Relativity confronted with Experiment", puis
séminaire spécialisé "Precision Tests of
Relativistic Gravity", Palerme, Italie.
Novembre 2005 : "Some generic problems with
MOND-like field theories", atelier "l'Univers primordial",
Montpellier.
Janvier 2006 : "Binary-pulsar tests of gravity
theories", atelier "Pulsars, théories et
observations", Paris.
Juin 2006 : "The theoretical significance of
gravity tests", colloquium de l'ENS de Lyon.
Octobre 2006 :
"Gravitation:
Theories and Experiments", cours avancé de 20
heures donné en collaboration avec C. Will (la
moitié chacun), dans le cadre du trimestre de
relativité générale au Centre émile
Borel (IHP, Paris).
Mars 2007 : "Pioneer, Anomalie
Einstein ?", débat public avec Jean
Einsenstaedt, Serge Reynaud et Cédric Deffayet, au
Réfectoire des Cordeliers, Paris.
Juillet 2007 : "Field-theoretical formulations of
MOND-like gravity", 18th International Conference on General
Relativity and Gravitation, GRG18, Sydney
(Australie).
Décembre 2007 : [même titre],
Centre de Physique Théorique, Marseille.
Mars 2008 : "Experimental and theoretical
constraints on alternative gravity theories", ESF
Exploratory Workshop on "Astrophysical Tests of Fundamental
Physics", Porto, Portugal.
Avril 2008 : conférence plénière
"Gravitation newtonienne modifiée et théorie
des champs", Journées du GDR Supersymétrie,
Strasbourg.
Juin 2008 : "Motion in alternative theories of
gravity", École thématique du CNRS sur la
Masse et "11th Capra Conference on Radiation Reaction",
Orléans.
Octobre 2008 : "Field-theoretical formulations of
MOND-like gravity", Département de physique
théorique, Université de Turin, Italie.
Novembre 2008 : "Gravitation newtonienne
modifiée et théorie des champs", cours de
4h30, IXe École de Cosmologie,
Cargèse.
Novembre 2008 : "Field-theoretical formulations
of MOND-like gravity", First Paris-Stockholm workshop on
consistent infrared modifications of gravity, Paris.
Novembre 2009 : "Vérifications
expérimentales de la relativité
générale", Institut de Mathématiques de
Jussieu, Paris.
Juin 2011 : "MOND-like field theories",
contribution à journée "Relativistic MOND versus
Cold Dark Matter", IAP, Paris.
Octobre 2012 : conférence
plénière "Binary-pulsar constraints on
(conformal & disformal) scalar-tensor gravity",
colloque international "From Quantum to Cosmos 5", Q2C5,
Cologne, Allemagne.
Avril 2013 : "Binary-pulsar constraints on
(conformally & disformally-coupled) scalar-tensor
gravity", atelier international "GRAMAP (GRAM And Pulsars)",
Paris.
Mai 2013 : "Time-dependent spherically symmetric
covariant Galileons", atelier international "Modern aspects
of gravity and cosmology", LPT, Orsay.
Avril 2014 : conférence plénière
"Binary pulsars and strong-field scalar-tensor gravity",
colloque international "The Strong Gravity Regime of Black Holes
and Neutron Stars", 558th WE-Heraeus Seminar, Bad Honnef
(Allemagne).
Juin 2015 : "Counting the degrees of freedom of
generalized Galileons", LPT, Orsay.
Octobre 2015 :
"Tester
la relativité générale", cycle de
conférences "L'Odyssée de l'espace-temps, 100 ans
de relativité générale", Palais de la
Découverte.
Janvier 2016 : "Tester la relativité
générale", Société Astronomique
de France.
Mai 2017 : "Self-tuning of the cosmological
constant in generalized Galileon/Horndeski theories",
atelier international "Hot topics in Modern Cosmology"
(Spontaneous Workshop XI), Cargèse.
[Version de janvier 2018]
Si la grande majorité de mes travaux de recherche concerne la gravitation, j'ai aussi consacré les années 1989–92 à la physique des particules. Mon point de vue était toutefois similaire, à savoir celui d'un théoricien des champs se servant de géométrie différentielle. La véritable réorientation thématique de ma carrière s'est en fait produite en 2000 lorsque j'ai quitté le Centre de Physique Théorique de Marseille pour aller au DARC de Meudon puis à l'Institut d'Astrophysique de Paris. J'ai alors ouvert mes recherches à plusieurs thèmes nouveaux pour moi : la cosmologie, les développements post-newtoniens à des ordres élevés, et l'étude de modèles modifiant la gravitation à grande distance. Bien qu'il s'agisse toujours de gravitation, les connaissances nécessaires et les outils mathématiques utilisés sont très différents de ceux de mes précédents travaux. Paradoxalement, c'est donc en restant dans ce thème de "la gravitation" que j'ai effectué un "changement thématique", car il ne s'agissait pas des mêmes aspects théoriques, alors que mes recherches au CPT sur les théories de Kaluza-Klein, en physique des particules et en géométrie non-commutative consistaient à appliquer les mêmes outils mathématiques à différents domaines.
Pour clarifier ce rapport, je présenterai mes travaux essentiellement par ordre chronologique, mais il peut aussi être utile d'en avoir d'abord un aperçu thématique. Les numéros indiqués sont ceux des chapitres suivants, et les références entre crochets renvoient à ma liste de publications.
Géométrie et physique des particules
Gravitation
Pour résumer l'ensemble de mes travaux, j'étudie diverses classes de théories des champs, en premier lieu de la gravitation, en cherchant à combiner les contraintes expérimentales et théoriques. Du point de vue phénoménologique, je tiens compte des tests dans le système solaire, des pulsars binaires, des détections directes d'ondes gravitationnelles, des courbes de rotation de galaxies & d'amas, et de l'évolution cosmologique du fond & des perturbations. Du point de vue mathématique, je cherche à identifier les degrés de liberté des différents modèles étudiés, pour analyser l'hyperbolicité de leurs équations de champs et donc déterminer si leur problème de Cauchy est bien posé, et j'étudie leur stabilité en analysant si leur densité de hamiltonien est bornée inférieurement. Si chacune de ces classes de contraintes est déjà assez forte pour exclure certains modèles proposés dans la littérature, c'est souvent leur prise en compte simultanée qui se révèle la plus efficace, et permet ainsi d'identifier la classe de théories la plus prometteuse pour décrire les différents aspects de notre Univers.
Ma thèse de doctorat [4] a été consacrée aux théories unifiées de la gravitation et de l'électromagnétisme obtenues par réduction dimensionnelle, d'abord en physique classique [1], puis en théorie quantique des champs [2, 3].
Dans l'article [1], en collaboration avec Robert Coquereaux, nous montrons que la théorie pentadimensionnelle de Kaluza-Klein est incompatible avec l'expérience si l'on suppose que les points matériels se déplacent le long des géodésiques de l'espace de dimension 5. En revanche, elle conduit aux mêmes paramètres post-newtoniens que la relativité générale si la matière est couplée à la métrique d'Einstein quadridimensionnelle : la présence du champ scalaire de Jordan-Thiry ne modifie la solution de Schwarzschild qu'à l'ordre post-post-newtonien. (Il est toutefois nécessaire de supposer que ce scalaire acquiert une masse ou que le potentiel Aμ de Kaluza ne décrit pas l'électromagnétisme pour que la théorie respecte le principe d'équivalence faible.) Dans la première partie de ma thèse [4], j'ai aussi généralisé cette étude aux théories de dimensions supérieures à 5, et aux champs matériels en première quantification, le cas des spineurs permettant d'éviter certains des problèmes mentionnés. L'un des intérêts de l'article [1] est d'avoir établi des formules exactes pour les solutions statiques à symétrie sphérique des théories tenseur-scalaire de la gravitation, qui m'ont été par la suite très utiles pour mes travaux en collaboration avec Thibault Damour [10-23].
Les articles [2] et [3] sont consacrés aux calcul des divergences à une boucle de cette même théorie de Kaluza-Klein en utilisant les méthodes du champ de fond, du développement de la chaleur et de la régularisation dimensionnelle, car il s'agit de théorie quantique des champs en espace courbe. Nous montrons qu'elle n'est pas renormalisable à une boucle, mais qu'il existe une sorte d'amélioration par rapport à la théorie d'Einstein-Maxwell : grâce au couplage du champ scalaire aux photons, de nouveaux diagrammes apparaissent et compensent certaines divergences du système gravitation+électromagnétisme. Outre l'exposé détaillé des techniques mathématiques nécessaires au calcul des 59 familles de diagrammes à une boucle de la théorie, la seconde partie de ma thèse [4] généralise ces résultats au cas d'un couplage quelconque entre le scalaire et les photons. Nous montrons notamment que parmi les théories gravitation+électromagnétisme+scalaire, celle de Kaluza-Klein conduit au coefficient le plus faible en facteur des termes divergents (dans le cas particulier où le champ de fond du scalaire est nul). Ainsi notre travail souligne une particularité du couplage scalaire-photon obtenu par réduction dimensionnelle, et permet d'avoir un éclairage nouveau sur l'annulation des divergences dans les théories supersymétriques et de dimensions supérieures.
Je me suis réintéressé à ce type de problèmes lors de mon séjour à l'Université de Brandeis (USA), en 1995–96. J'ai par exemple démontré que le système Einstein-modèle-sigma n'est jamais fini à une boucle, quel que soit le modèle-sigma considéré, bien que les termes divergents n'aient pas tous le même signe. En collaboration avec S. Deser, j'ai aussi montré que la solution de Schwarzschild de la relativité générale ne peut pas provenir de la réduction dimensionnelle d'une métrique non singulière, même si la théorie extra-dimensionnelle contient un dilaton en plus de sa métrique. Un autre sujet voisin a été de montrer qu'il existe des théories de la gravitation compatibles avec la force de Newton (donc attractives) mais pourtant exemptes d'horizons. En revanche, si la théorie contient au moins un champ de spin 2, ou plus simplement si l'on veut qu'elle soit compatible avec les tests post-newtoniens, alors elle conduit nécessairement à l'existence d'horizons. S. Deser et moi-même avons trouvé des démonstrations courtes et élégantes de ces résultats, mais n'avons pas jugé crucial de les publier. J'ai également démarré à Brandeis des recherches sur la gravitation en dimension 3 et sur les intersections de p-branes en dimension 10, qui ont enrichi ma connaissance des théories unifiées et extradimensionnelles.
Ces connaissances, et notamment celle de la régularisation dimensionnelle, se sont avérées fort utiles pour mes travaux consacrés au développement post-newtonien de la relativité générale (paragraphe VI.1).
Les articles [5] et [7] montrent qu'une étude de la structure géométrique du groupe de Lie SU(3) – considéré comme variété – peut être très utile, non seulement pour l'interprétation de quantités physiques mais aussi pour la clarification et la simplification du calcul de diagrammes de Feynman.
L'objet de la lettre [5] est de classifier toutes les métriques invariantes sur SU(3) en les décomposant sur des espaces de dimensions 1+8+27, ainsi que les structures riemanniennes associées en indiquant le nombre de paramètres réels dont elles dépendent, ce qui permet de caractériser la brisure de symétrie SU(3) × SU(3). Les masses des bosons formés à partir des quarks (u,d,s) peuvent être considérées comme les valeurs propres de l'opérateur laplacien sur SU(3), et le cas particulier d'une métrique invariante par [SU(2)I × U(1)Y] × SU(3) nous permet d'établir une généralisation de la formule de Gell-Mann-Okubo. La formule habituelle est retrouvée lorsque la métrique n'a pas de composante dans la représentation de dimension 27. L'écart entre la masse expérimentale du méson pseudo-scalaire η et celle prédite par cette formule est expliqué dans la littérature en introduisant un angle de mélange entre le η et le η'. Notre approche géométrique donne une autre interprétation de cet écart, qui mesure la brisure de symétrie due à la composante 27 de la métrique.
L'article [7] est consacré au calcul des divergences à une boucle du lagrangien effectif décrivant les interactions fortes et faibles non leptoniques des mésons pseudo-scalaires, dans le formalisme des perturbations chirales. Nous montrons que tenir compte des interactions faibles revient à choisir une métrique (invariante à droite) quelconque sur SU(3), alors que les interactions fortes correspondent à la métrique de Killing (invariante à droite et à gauche). Une interprétation géométrique des divergences à une boucle en termes de tenseurs de courbure, grâce aux techniques du développement de la chaleur, permet donc de traiter simultanément les interactions fortes et faibles. Outre leur clarté et leur relative simplicité, nos calculs nous ont permis de corriger certains résultats de la littérature. Nous montrons également que cette approche géométrique conduit de façon naturelle à un modèle permettant de relier entre elles les différentes constantes de couplage du lagrangien effectif à l'ordre O(p4). Les relations que nous obtenons sont indépendantes du choix de l'échelle de renormalisation μ.
Cette approche géométrique de la physique des particules se retrouve dans les modèles de gravitation modifiée sur lesquels je travaille actuellement.
Dans les articles [6] et [8] en collaboration avec R. Coquereaux, F. Scheck (Mainz, Allemagne) et G. Vaillant, ainsi que dans la conférence [9], nous montrons que la totalité du lagrangien du modèle standard des interactions électro-faibles peut être retrouvée de façon très naturelle, en utilisant la géométrie différentielle non-commutative et la théorie des algèbres de Lie graduées.
L'article [6] est consacré au lagrangien bosonique, et retrouve en des termes extrêmement simples les résultats d'A. Connes et J. Lott (qui nécessitaient des outils mathématiques complexes et des calculs assez techniques). Les bosons de jauge et les champs de Higgs peuvent être unifiés dans une seule (super-) connexion, définie sur deux espaces-temps parallèles, et le lagrangien s'écrit alors comme une théorie de Yang-Mills pure. Les champs de Higgs apparaissent comme les bosons de jauge associés à la symétrie discrète qui échange les espaces "gauche" et "droit". Le modèle standard peut ainsi être considéré comme un analogue discret des théories de Kaluza-Klein, où les dimensions supplémentaires sont remplacées par un ensemble de deux points. Outre la reformulation esthétique de la théorie de Glashow-Salam-Weinberg qu'apporte un tel formalisme, il permet également de réduire son arbitraire (en prédisant notamment la forme du potentiel de Higgs et un angle de Weinberg égal à celui obtenu dans les théories de grande unification).
Cette remarque s'applique aussi à l'article [8], consacré au lagrangien fermionique. Nous montrons que la superconnexion précédente correspond à la représentation adjointe de l'algèbre de Lie graduée SU(2|1), et que ses représentations typique et atypique de plus basses dimensions décrivent les quarks et les leptons. Cette constatation avait déjà été faite dans les différentes tentatives des années 80 pour "jauger" SU(2|1), mais le lagrangien n'avait jamais pu être retrouvé exactement. Notre synthèse [8] des idées de Connes et de Ne'eman montre que cela est non seulement possible mais naturel. Nous soulignons également que l'existence de représentations réductibles indécomposables conduit au mélange des saveurs des quarks, et fournit donc un cadre mathématique pour relier les masses de ces derniers aux angles de Cabibbo-Kobayashi-Maskawa. Nous montrons enfin qu'il est nécessaire d'introduire des formes différentielles de degrés quelconques dans la superconnexion pour pouvoir définir une action de SU(2|1) sur le lagrangien, mais que même dans une telle théorie généralisant le modèle standard, le lagrangien bosonique n'est invariant que par SU(2) × U(1), bien que le lagrangien fermionique le soit par toute la superalgèbre.
À la suite de nos travaux et de ceux de collègues du CPT, cette approche non-commutative de la physique des particules a été fortement développée à Marseille. Bien que je ne travaille plus directement sur ce thème, j'ai continué plusieurs années à suivre ses progrès attentivement. Dans un séminaire de mars 1997, j'ai par exemple étudié les conséquences du couplage non minimal du champ de Higgs à la gravitation prédit par le "principe spectral" de Chamseddine et Connes : il n'y a plus brisure spontanée de la symétrie SU(2) à l'échelle d'énergie où est écrit le lagrangien (à moins de choisir une fonction non monotone pour pondérer le comptage des valeurs propres de l'opérateur de Dirac).
De 1991 à 1998, mes travaux en collaboration avec Thibault Damour (IHÉS) ont été consacrés à l'étude des théories relativistes de la gravitation et à leurs tests expérimentaux. Notre but n'est pas de proposer de "meilleures" théories que la Relativité Générale (RG), mais de déterminer quelles propriétés de la théorie d'Einstein ont déjà été testées, et de proposer de nouvelles expériences pour mettre en lumière les aspects encore inexplorés. Pour cela, la méthode la plus efficace consiste à comparer entre elles plusieurs théories, RG comprise. On se rend alors compte que les tests classiques ne permettent pas de distinguer certaines de ces théories, et qu'il est donc nécessaire soit d'augmenter la précision des observations usuelles, soit d'imaginer de nouveaux tests capables de lever les ambiguïtés.
Le long article [10] est consacré à l'étude des théories dans lesquelles l'interaction gravitationnelle est transmise à la fois par un tenseur métrique gμν (de spin 2) et un ou plusieurs champs scalaires φa (de spin 0). Ces théories "tenseur-scalaire" apparaissent naturellement dans les tentatives théoriques de quantification de la gravitation ou d'unification avec les autres interactions (Kaluza-Klein, supercordes), dans les extensions non-minimales de la relativité générale (théories en R+R2+...), et dans les scénarios cosmologiques les plus crédibles (inflation et quintessence notamment). De plus, contrairement à toutes les autres alternatives à la relativité générale proposées dans la littérature, ces théories ne présentent aucune incohérence. En effet, elles ne nécessitent aucun ajustage fin de paramètres (no fine tuning), n'ont aucun champ adynamique ni degré de liberté d'énergie négative (no ghost), et leur problème de Cauchy est bien posé ; ce sont les seules théories de champs de masses nulles qui peuvent respecter exactement le principe d'équivalence faible (universalité de la chute des corps non autogravitants) ; ce sont les seules théories connues pour lesquelles la physique gravitationnelle reste invariante de Lorentz même en présence de corps massifs extérieurs ; enfin, elles expliquent le rôle-clef des paramètres β et γ dans le formalisme "post-newtonien paramétrisé" (tous les autres paramètres "PPN" sont nuls).
Notre article [10] étudie en détail les prédictions de ces théories tenseur-scalaire dans le formalisme "post-Keplerien", c'est-à-dire au premier ordre en v2/c2 pour les mouvements orbitaux, mais en tenant compte de tous les ordres en puissances des "compacités" des corps (énergies de liaison gravitationnelles divisées par mc2). En effet, ces compacités peuvent prendre des valeurs non négligeables pour des corps très condensés, comme les étoiles à neutrons, et une troncation au premier ordre ne serait plus justifiable. Nous établissons le lagrangien décrivant le mouvement de N corps autogravitants, puis calculons le rayonnement gravitationnel de tels systèmes (incluant les termes monopolaire, dipolaire et quadrupolaire dus à l'émission d'ondes scalaires, en plus du quadrupôle habituel de la relativité générale).
Nous montrons que contrairement à la théorie de Brans-Dicke, qui n'incorpore qu'un seul champ scalaire couplé de façon exponentielle à la matière, les théories comptant plusieurs scalaires ou les couplant de façon plus complexe peuvent être très différentes de la relativité générale en champs forts (au voisinage d'étoiles à neutrons) même si elles sont compatibles avec toutes les données expérimentales en champs faibles (dans le système solaire). Il est donc nécessaire d'observer des systèmes d'étoiles condensées tels que les pulsars binaires pour distinguer les prédictions de ces théories de celle d'Einstein.
Comme illustration, nous étudions une classe de théories comportant deux scalaires, couplés à la matière de telle sorte que leurs effets se compensent dans le système solaire. Nous montrons qu'un sous-ensemble de ces théories est non seulement compatible avec tous les tests expérimentaux en champs faibles, mais également avec le plus précis de ceux dont nous disposons en champs forts (le test "γ–ω̇–Ṗ" pour le pulsar binaire PSR 1913+16, qui a valu le prix Nobel à Hulse & Taylor en 1993). Nous soulignons donc que ce test n'est pas suffisant, et qu'il est nécessaire de combiner les données de plusieurs pulsars binaires pour contraindre l'espace des théories permises. Nos résultats théoriques ont immédiatement été utilisés par Damour & Taylor pour effectuer de nouveaux tests de la gravitation en champs forts, à l'aide d'autres pulsars binaires découverts entre temps.
Outre cette confrontation avec l'expérience, notre étude approfondie des théories tenseur-multi-scalaire conduit également à une paramétrisation des effets gravitationnels en champs forts, qui peut être considérée comme une généralisation du formalisme "PPN" aux ordres supérieurs. Cela permet d'étudier de façon très précise la violation du principe d'équivalence fort (influence de l'auto-gravitation des corps sur leur mouvement dans un champ extérieur), et de suggérer de nouveaux tests de la relativité générale, comme ceux de Damour & Taylor ou ceux que nous présentons ci-dessous.
En conclusion, notre article [10] est à l'origine de nombreux travaux tant expérimentaux que théoriques, allant des analyses de données de pulsars binaires jusqu'aux importantes études cosmologiques de Damour, Nordtvedt, Polyakov et Veneziano.
L'une des caractéristiques des théories tenseur-(multi)-scalaire est de ne prédire aucune violation de l'invariance de Lorentz locale de la physique gravitationnelle, c'est-à-dire de ne privilégier aucun référentiel. Les théories incorporant des champs vectoriels ou tensoriels (en plus de gμν) dans l'interaction gravitationnelle prédisent au contraire que notre vitesse par rapport au reste de l'Univers influence la physique locale. Vérifier expérimentalement l'invariance de Lorentz, en cherchant à contraindre le paramètre post-newtonien "α1", est donc une manière indirecte de tester l'hélicité des différents degrés de liberté a priori contenus dans l'interaction gravitationnelle. L'article [12] calcule les bornes sur ce paramètre fournies par les données des pulsars binaires. Nous montrons que s'il existe un référentiel privilégié, le périastre des orbites est "polarisé" dans une direction déterminée, et un calcul statistique nous permet ainsi de déterminer des limites précises sur α1. Outre le fait que nous corrigeons un résultat erroné de la littérature, l'intérêt de cet article est d'obtenir des contraintes sur l'invariance de Lorentz de la gravitation en champs forts. Nos résultats théoriques ont par la suite été utilisés par différents groupes pour analyser de nouvelles données de pulsars binaires.
Dans l'article [15], nous montrons que des limites sur α1 plus précises encore peuvent être obtenues en observant les orbites de satellites artificiels terrestres. En effet, si leur inclinaison et leur altitude sont bien choisies, les effets dus à ce paramètre sont amplifiés (apparition de petits diviseurs), donnant lieu à une évolution complexe du vecteur excentricité de l'orbite (somme de plusieurs rotations indépendantes) et à une oscillation annuelle de la longitude du satellite. Grâce à la technologie actuelle qui permet de mesurer la position de satellites artificiels avec une précision de l'ordre du centimètre, nous montrons que l'observation de telles orbites pourrait réduire de deux ordres de grandeur les limites sur α1. Certaines missions orbitales consacrées à d'autres tests de la gravitation ont été programmées pour des orbites très voisines de celles que nous proposons. Leur observation pourra donc fournir de nouvelles contraintes sur l'existence d'un référentiel privilégié.
L'article [16] montre que l'observation de satellites artificiels terrestres d'orbites basses peut également être très utile pour mesurer avec précision les paramètres post-newtoniens β et γ, qui sont les deux seuls à différer des valeurs de la relativité générale (β = γ = 1) dans les théories tenseur-scalaire de la gravitation. Contrairement au cas de la Lune, pour laquelle l'effet Nordtvedt (violation du principe d'équivalence fort) est le plus important, les deux effets prédominants pour les satellites bas sont l'avance relativiste du périgée, et l'oscillation annuelle de la longitude due à une variation de la constante de gravitation effective. Ici encore, l'utilisation de la technologie actuelle pour déterminer à un centimètre près la position d'un satellite pendant un an, devrait permettre de réduire d'un ordre de grandeur les limites sur β et γ, et de gagner deux ordres de grandeur sur la détermination de la variation temporelle de la constante de gravitation Ġ/G. Nos résultats ont été pris en compte dans la programmation de futures missions orbitales.
L'article [17], résultat d'un travail de plus d'un an (1994–95), est consacré aux effets gravitationnels possibles à l'ordre post-post-newtonien (1/c4 par rapport à la force newtonienne, ou "2PN"). Au lieu de chercher à décrire a priori n'importe quelle théorie de la gravitation imaginable, comme la littérature existante essayait de le faire de façon incomplète et souvent erronée, nous nous sommes restreints à celles qui soient des théories des champs, et parmi celles-ci aux seules connues qui ne présentent aucune incohérence : les théories "tenseur-(multi)-scalaire", dont nous avions déjà effectué une étude détaillée à l'ordre 1/c2 en 1991–92 [10].
Le fait de nous restreindre à cette classe de théorie nous a permis d'étudier de façon systématique tous les effets possibles à l'ordre 1/c4. Nous avons pour cela développé une technique diagrammatique qui clarifie considérablement l'analyse. Notre résultat principal est qu'en plus des paramètres d'Eddington β et γ, seuls deux nouveaux paramètres sont nécessaires pour décrire tous ces effets post-post-newtoniens, alors que la littérature en utilisait une dizaine. Nous les avons notés ε et ζ, par analogie avec les diagrammes dont ils proviennent. Notre approche de théorie des champs nous a également permis de démontrer facilement certaines relations entre les différents paramètres, par exemple ζ ≥ 8 (β–1)2 / |γ–1|, et surtout le fait que (β–1), ε et ζ [ainsi que tout nouveau paramètre apparaissant aux ordres supérieurs] tendent vers 0 avec (γ–1). Cela souligne l'importance fondamentale de (γ–1), qui mesure le carré du couplage linéaire entre la matière et le(s) scalaire(s).
D'un point de vue plus expérimental, nous avons montré qu'ε et ζ n'interviennent pas à l'ordre 2PN dans la déviation de la lumière ou dans le retard des échos radar. Cela signifie que les expériences ultra-précises prévues pour les années à venir dans le système solaire ne pourront mettre en évidence aucun nouvel effet 2PN, mais qu'elles permettront justement de déterminer γ sans avoir à se soucier des ordres supérieurs de la théorie. En revanche, ces déviations post-post-newtoniennes sont importantes dans les étoiles à neutrons, et notre analyse des données de quatre pulsars binaires donne déjà les contraintes |ε| < 7×10–2, |ζ| < 6×10–3. Nos résultats théoriques ont par la suite été utilisés par d'autres chercheurs pour l'analyse des données de différents pulsars binaires.
Mentionnons aussi qu'au cours de notre étude, nous avons obtenu plusieurs résultats utiles même en dehors du cadre des théories tenseur-scalaire. Par exemple, nous donnons dans un appendice de [17] l'expression de l'avance du périhélie à l'ordre 1/c4 dans toute théorie métrique de la gravitation. Nous avons également démontré la forme exacte (c.-à-d. à tous les ordres en puissances de 1/c) du théorème du viriel reliant l'énergie gravitationnelle d'un corps à sa pression, valable en relativité générale et en théorie de Brans-Dicke.
Les résultats du paragraphe précédent montrent que les théories tenseur-scalaire de la gravitation sont perturbativement équivalentes à la relativité générale si γ = 1, c'est-à-dire s'il n'y a pas de couplage linéaire entre la matière et le scalaire. Dans des conditions de champs gravitationnels faibles (système solaire), de telles théories ne présentent donc aucune déviation par rapport à la théorie d'Einstein, à tous les ordres en puissances de 1/c. Cependant, comme nous le montrons dans la série d'articles [13, 18, 21], des effets non perturbatifs peuvent tout de même se produire en champs forts, notamment au voisinage d'étoiles à neutrons.
Dans la lettre [13], nous supposons que le paramètre d'Eddington γ est suffisamment proche de 1 pour que la théorie tenseur-scalaire considérée passe tous les tests du système solaire. Nous montrons pourtant que certains couplages quadratiques de la matière au champ scalaire conduisent à des effets très différents de ceux de la relativité générale en champs forts. Nous l'expliquons à l'aide d'un raisonnement analytique approché, et confirmons notre analyse par une intégration numérique des équations différentielles couplées de la métrique, du champ scalaire, et de polytropes décrivant correctement la matière nucléaire. Nous soulignons que de telles théories sont très naturelles, car elles ne nécessitent aucun ajustage fin de paramètres ("no fine-tuning") ni aucune grande valeur numérique de ceux-ci, et elles ne contiennent bien sûr aucun champ adynamique ni degré de liberté d'énergie négative.
Dans l'article [18], écrit lors de mon année à l'Université de Brandeis (T. Damour se trouvant alors à l'Institute for Advanced Study de Princeton), nous interprétons les effets non perturbatifs précédents comme un analogue gravitationnel de la magnétisation spontanée des matériaux ferromagnétiques : au-delà d'une masse critique, il est énergétiquement favorable à une étoile à neutrons de se "scalariser" spontanément. Même si le champ scalaire de fond est strictement nul (γ = 1, donc aucune différence par rapport à la relativité générale en champs faibles), la physique des corps compacts peut ainsi dévier de façon significative des prédictions de la théorie d'Einstein.
Cet article [18] complète aussi les résultats de [13] en montrant comment calculer le moment d'inertie d'une étoile dans ce cadre théorique, ainsi que sa variation due à la présence d'un corps compagnon. Ces quantités physiques, assez subtiles à définir, sont en effet nécessaire pour prédire le retard des ondes radio émises par un pulsar. [Elles sont d'ailleurs liées à un comportement paradoxal d'une classe de ces théories : plus elles sont proches de la relativité générale dans le système solaire, plus elles en diffèrent au voisinage d'étoiles à neutrons.]
Le résultat principal de notre étude est que les tests des pulsars binaires sont qualitativement différents des tests de la gravitation effectués dans le système solaire. En effet, notre analyse de trois pulsars binaires nous a permis d'éliminer toute une classe de théories qui sont indistinguables de la relativité générale en champs faibles (à tous les ordres). Nous montrons que les théories compatibles avec l'ensemble des données expérimentales sont telles que (β–1)/(γ–1) < 1.1, où β ≃ 1 et γ ≃ 1 sont les paramètres post-newtoniens d'Eddington. Il est heureux de constater que l'espace des théories permises inclut précisément celles qui sont privilégiées par les études cosmologiques de Damour, Nordtvedt, Polyakov et Veneziano.
L'article [21] confirme et complète les résultats précédents en considérant plusieurs équations d'état réalistes pour décrire la matière nucléaire constituant les étoiles à neutrons, dans nos programmes d'intégration numérique. Nous analysons également les effets possibles dus à la taille finie des étoiles (c.-à-d. au fait qu'elles ne sont pas des points matériels), en utilisant notre technique diagrammatique de [17] qui simplifie considérablement les précédents résultats de K. Nordtvedt.
Nous montrons que le système idéal pour tester les théories tenseur-scalaire de la gravitation serait un pulsar orbitant autour d'un trou noir. Son observation devrait permettre d'augmenter de trois ordres de grandeur la précision des tests actuels sur γ–1. Nos travaux soulignent donc l'importance de la recherche de nouveaux pulsars binaires par les différentes équipes expérimentales, comme celle de J. Taylor à Princeton.
Mentionnons pour finir que nos travaux [13, 18, 21] ont été à l'origine d'un bon nombre d'articles théoriques sur la "scalarisation spontanée", notamment par une équipe japonaise ; la thèse de Jérôme Novak y a aussi été consacrée à Meudon, en mars 1998. Mon collègue de l'IAP, Enrico Barausse, ainsi que ses collaborateurs, y ont également consacré plusieurs articles ces dernières années.
Nous avons indiqué quelques résultats de notre article [21] ci-dessus, mais son but principal est surtout de comparer les contraintes imposées par les différents types d'expériences gravitationnelles dans le cadre des théories tenseur-scalaire : tests dans le système solaire [champs faibles], tests des pulsars binaires [champs forts], et futures détections de binaires spiralantes avec les interféromètres LIGO & VIRGO [effets de champs forts détectés en champs faibles]. En raison du faible couplage de la matière au champ scalaire (γ–1 ≃ 0), il est presque certain que ces interféromètres ne pourront détecter aucune onde d'hélicité 0. Mais comme C. Will l'a souligné en 1994, l'évolution temporelle du signal d'hélicité 2 détecté ("chirp") dépendra de la dynamique du système binaire en champs forts, et donc de la présence d'un partenaire scalaire du graviton. En raison du phénomène de "scalarisation spontanée" décrit plus haut, ces interféromètres seront donc plus sensibles à la présence d'un champ scalaire que les tests classiques dans le système solaire. Cependant, nous montrons dans [21] que les données actuelles des pulsars binaires sont si précises qu'elles excluent déjà les théories pour lesquelles des effets scalaires auraient pu être observables avec LIGO & VIRGO. Paradoxalement, ce résultat est une bonne nouvelle, car il justifie que l'on se restreigne à la relativité générale pour calculer les formes d'ondes gravitationnelles à détecter (travail d'une extrême difficulté même dans le cadre "simple" de la théorie d'Einstein). Il est important de souligner que les projets LIGO & VIRGO gardent tout leur intérêt, non seulement pour la détection directe d'ondes gravitationnelles mais également comme nouvelles fenêtres observationnelles de la structure interne des étoiles et de leur dynamique lors de coalescences. Notre travail montre seulement que les pulsars binaires sont d'une précision inégalable pour contraindre l'existence de partenaires scalaires du graviton.
Les conclusions de notre article [20] soulignent à quel point les projets LIGO & VIRGO sont importants. En effet, plusieurs publications récentes prétendaient que les ondes gravitationnelles sont observables sans utiliser de tels coûteux interféromètres. L'idée était d'observer par des moyens astrométriques la déflexion de la lumière par des ondes gravitationnelles. Si ces ondes sont suffisamment éloignées de la Terre, on pourrait s'attendre à des effets non négligeables, car un angle de déflexion minuscule peut conduire à de grands déplacements apparents de la source lumineuse. Cependant, nos calculs précis (tenant compte à la fois de la zone proche de la source de rayonnement gravitationnel, de la zone intermédiaire, et de la zone d'onde) montrent sans ambiguïté que la déflexion en question est en 1/b3, où b est le paramètre d'impact du rayon lumineux, et non en 1/b comme la littérature le prétendait. Autrement dit, les effets sont bien trop faibles pour être accessibles à l'astrométrie actuelle, et les grands projets LIGO & VIRGO sont donc nécessaires. [Kopeikin, Schäfer, Gwinn et Eubanks ont par la suite confirmé nos résultats en utilisant une autre méthode de calcul.]
Les tests de la gravitation sont devenus considérablement plus précis depuis 2003. Non seulement de nouvelles contraintes ont été obtenues dans le système solaire (observation de la sonde Cassini près de sa conjonction avec le Soleil, et données améliorées du "Lunar Laser Ranging"), mais deux nouveaux pulsars binaires très relativistes ont été chronométrés avec précision. L'un d'eux, PSR J1141–6545, est constitué d'une étoile à neutrons et d'une naine blanche, et malgré les incertitudes initialement importantes sur la diminution de sa période orbitale, il s'est immédiatement révélé comme le système le plus contraignant pour les théories tenseur-scalaire de la gravitation. En effet, elles prédisent de façon générique un fort rayonnement dipolaire pour un tel système très dissymétrique, ce qui est incompatible avec la faible valeur de son accélération orbitale. L'autre système, PSR J0737–3039, est exceptionnel pour plusieurs raisons, en particulier parce que les deux étoiles sont observées comme des pulsars. Cela permet une détermination directe du rapport de leurs masses, et donc d'effectuer un nouveau test de la gravitation en champ fort, indépendant de tous les autres tests connus.
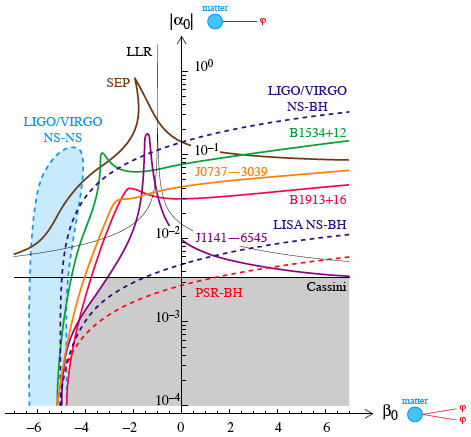
Dans les conférences [33, 30] et le cours [35], j'ai analysé les nouvelles contraintes que de telles données imposent sur les théories tenseur-scalaire. Cette étude est d'une grande importance pour les expérimentateurs, car elle illustre la qualité de leurs mesures et souligne leur intérêt théorique. Seuls mes programmes permettaient de calculer ces contraintes. Notre méthode a bien sûr été expliquée en détail dans nos articles [13, 18, 21] en collaboration avec Thibault Damour, mais les différentes équipes qui ont par la suite travaillé sur ce sujet se sont concentrées sur quelques effets seulement. Or les dérivées des charges scalaires et des moments d'inertie interviennent aussi dans les quantités observables, donc il faut savoir les calculer, et cela nécessite des programmes assez complexes. Les contraintes imposées par le système solaire sont d'ailleurs devenues si fortes que j'ai dû moi-même réécrire mes anciens programmes, car certaines dérivées divergent quand le couplage de la matière au champ scalaire tend vers zéro (voir le chapitre IV.4 ci-dessus). J'ai donc passé une partie importante de l'année 2005 à tout reprogrammer en détail, en me servant de la vitesse des ordinateurs actuels pour améliorer la précision et la quantité de tests effectués. Il me faut insister sur le fait que c'est un travail considérable, à la fois en nombre d'heure et en taille des fichiers (donnant les facteurs de forme des étoiles à neutrons dans chacune des théories considérées).

Le résultat final de ces programmes volumineux est une mise à jour de toutes les contraintes expérimentales sur les théories tenseur-scalaire de la gravitation. La figure ci-dessus souligne en particulier que les dernières données du pulsar binaire dissymétrique J1141–6545 donnent des contraintes qui rivalisent avec celles du système solaire dans presque tout l'espace de théories.
J'ai de nouveau mis à jour ces contraintes en 2012, dans l'article [47] en collaboration avec l'équipe des radioastronomes du Max Planck Institut de Bonn. Elles sont encore plus fortes grâce au nouveau système pulsar-naine blanche PSR J1738+0333. Nous avons également calculé les contraintes qu'il impose sur les théories de type TeVeS (cf. chapitre VII ci-dessous), dans lesquelles le couplage matière-scalaire est non conforme. J'ai recommencé ces mises à jour plusieurs fois ces dernières années, quand les radioastronomes me fournissait de nouvelles données observationnelles. Dans la figure ci-dessous, tracée pour une conférence, j'ai notamment utilisé des données du double pulsar PSR J0737–3039 bien plus récentes que dans l'article [47].
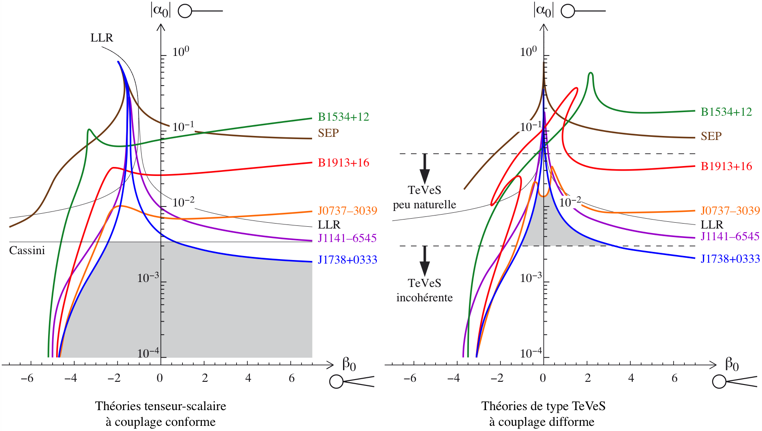
Un article en collaboration avec M. Kramer, N. Wex, T. Damour et I. Stairs (entre autres) est envisagé depuis plusieurs années, mais je suis dépendant de l'emploi du temps des radioastronomes, qui repoussent régulièrement son écriture. J'utiliserai évidemment les toutes dernières données du double pulsar PSR J0737–3039, qui ont encore été améliorées par rapport à la figure ci-dessus. Il me faudra par ailleurs retracer ces figures en utilisant une équation d'état plus dure pour la matière nucléaire, afin de tenir compte de l'existence d'étoiles à neutrons très massives (découvertes elles-mêmes grâce à l'observation de pulsars binaires). Les contraintes que tous ces pulsars binaires imposent sur les théories de Brans-Dicke à champ scalaire massif seront aussi tracées. Le double pulsar est remarquablement contraignant pour cette classe de théories — alors que le plus intéressant pour les théories tenseur-scalaire sans masse est le système pulsar-naine blanche PSR J1738+0333, comme illustré ci-dessus. Il est intéressant de noter que les divers pulsars binaires observés sont ainsi complémentaires, ne donnant pas les mêmes informations selon les classes de théories considérées.
Mentionnons enfin le cours [39], dans lequel je me suis servi de cet exemple des théories tenseur-scalaire pour illustrer divers aspects de la gravitation relativiste, notamment le théorème de la calvitie (no-hair) des trous noirs, les effets de taille finie et le principe d'effacement en relativité générale, et le fait que la dynamique du champ gravitationnel influe directement sur le mouvement des corps matériels.
Les observations de supernovæ de type Ia à grands décalages vers le rouge (z ~ 1) indiquent que l'univers est en expansion accélérée. Cela peut être expliqué par une valeur non nulle de la constante cosmologique Λ. Cependant, la très faible valeur qu'elle doit prendre (≃ 3×10–122 c3/ℏG) ne trouve d'explication naturelle que dans le cadre de la "quintessence", où elle apparaît comme la valeur actuelle du potentiel d'un champ scalaire, attiré vers le minimum au cours de son évolution cosmologique. De nombreux articles des années 2000 ont examiné les conséquences observables de certaines formes bien particulières d'un tel potentiel. A. Starobinsky a au contraire adopté un point de vue phénoménologique : il a montré comment reconstruire le potentiel grâce aux données expérimentales. Dans notre lettre [24], nous avons généralisé ce point de vue à une théorie tenseur-(mono)-scalaire quelconque. Nous montrons que les deux fonctions inconnues du champ scalaire dont dépend le lagrangien (potentiel et fonction de couplage scalaire-matière) peuvent être reconstruites de façon unique à partir de la donnée de deux fonctions observables du décalage vers le rouge z : la distance-luminosité, et le contraste de densité de la matière poussiéreuse. Les observations cosmologiques pourront donc fournir des informations sur la forme complète de ces fonctions, alors que les tests classiques de la gravitation (aussi bien dans le système solaire qu'avec les pulsars binaires) ne contraignent que leurs valeurs actuelles et leurs premières dérivées.
Le plus long article [25], en collaboration avec David Polarski, approfondit ces résultats de plusieurs façons. Nous écrivons tout d'abord l'action de la théorie dans une paramétrisation quelconque, et donnons les équations correspondantes ; cela permet de comparer facilement entre eux les divers résultats de la littérature. Nous généralisons aussi notre lettre [24] au cas d'univers spatialement courbes, et au cas d'une pression non nulle pour la matière. Mais notre but est surtout d'étudier les contraintes observationnelles sur de tels modèles. Comme la distance-luminosité (en fonction du décalage vers le rouge z) sera déterminée avec précision plus rapidement que la croissance du contraste de densité de la matière, au cours des prochaines années, nous analysons quels types de théories seront testées par la seule connaissance de cette première fonction. Nos résultats, à la fois analytiques et numériques, montrent que sa mesure sur un intervalle significatif de z (par exemple entre 0 et 2) sera en fait plus contraignante que la précision même des mesures. L'argument crucial de notre analyse, oublié dans la plupart des articles publiés dans ce domaine, est la positivité de l'énergie du graviton et du champ scalaire, afin que la théorie soit stable et mathématiquement cohérente. Cette contrainte théorique, alliée à celles imposées par les données expérimentales du système solaire et des pulsars binaires (voir le chapitre IV), suffit en effet pour interdire toute une classe de théories au-delà de redshifts de l'ordre de 2. Nous montrons notamment que les données du satellite SNAP devraient suffire pour distinguer les prédictions de la relativité générale (plus constante cosmologique) de celles de théories de quintessence à champ scalaire de masse nulle, donc de confirmer ou d'infirmer la présence d'un tel scalaire. Dans le cadre complémentaire des théories à scalaire massif mais minimalement couplé à la gravitation, nous calculons l'expression analytique du potentiel du champ scalaire permettant de reproduire la même fonction de Hubble H(z) qu'en relativité générale plus constante cosmologique. Dans ce cas, nous trouvons que les modèles les plus naturels sont obtenus si l'univers est marginalement fermé (tout en restant compatible avec les données observationnelles).
Les théories tenseur-scalaire les plus générales peuvent dépendre de davantage de fonctions a priori inconnues du champ scalaire. En plus d'un potentiel et d'une fonction de couplage à la matière, le champ scalaire peut en effet être aussi couplé à l'invariant topologique de Gauss-Bonnet, ce qui se produit de façon générique dans les théories de cordes. Les autres couplages à des puissances de la courbure entraînent l'apparition de degrés de liberté supplémentaires, correspondant soit à d'autres champs scalaires (sortant donc du cadre mono-scalaire que nous avons choisi d'étudier), soit à des champs massifs de spin 2 et d'énergie cinétique négative (de tels fantômes rendant le modèle instable). En 2001–2002, j'ai dirigé la thèse de laurea d'une étudiante italienne, Elisabetta Semboloni, pour analyser quel type de contraintes expérimentales peut être obtenu sur un tel couplage scalaire-Gauss-Bonnet.
Nous nous sommes restreints à un modèle sans potentiel ni couplage scalaire-matière, et avons effectué une analyse analogue à celle de mon précédent travail en collaboration avec D. Polarski. De nouveau, nous avons trouvé que la combinaison des données cosmologiques et des expériences dans le système solaire est très contraignante, mais pour des raisons assez subtiles. Tout d'abord, le modèle peut facilement être compatible avec l'une de ces classes d'observations si l'on ne tient pas compte de l'autre. De plus, on peut montrer que la théorie est attirée vers la relativité générale au cours de l'évolution cosmologique de l'univers. Mais à cause d'effets fortement non-linéaires, les tests du système solaire s'avèrent extrêmement contraignants, et il est impossible de les satisfaire si l'univers est actuellement dans une phase d'expansion accélérée. Ces effets non-linéaires, qu'on aurait naïvement négligés, nous permettent donc finalement d'éliminer ce modèle a priori concurrent de la relativité générale plus constante cosmologique. Évidemment, les modèles comportant deux ou trois fonctions du champ scalaire peuvent être compatibles avec toutes les données observationnelles, puisqu'ils englobent les théories de quintessence (étendue). La présence d'un couplage scalaire-Gauss-Bonnet modifie dans ce cas le comportement de la théorie à petite échelle (Big Bang, croissance des structures).
J'ai présenté ces résultats dans plusieurs conférences, dont certaines ont donné lieu à des actes [28], et notamment dans l'article [33] qui est une revue de mes divers travaux sur les théories tenseur-scalaire. Notre étude du couplage scalaire-Gauss-Bonnet a par la suite été reprise et généralisée par Amendola, Charmousis et Davis.
L'article [41], en collaboration avec Cyril Pitrou & Jean-Philippe Uzan, date de 2009 et est donc postérieur à plusieurs travaux des chapitres VI et VII.1 ci-dessous. Il me semble toutefois préférable de le résumer après mes études des théories de quintessence étendue.
Les théories que nous avons analysées généralisent en effet les scalaires de la quintessence à des champs vectoriels. La raison principale pour laquelle de tels vecteurs intéressent les cosmologues est qu'ils peuvent a priori engendrer des anisotropies du fond micro-onde cosmologique et des grandes structures. Toutefois, dans les modèles les plus simples, la valeur de fond du vecteur tend rapidement vers zéro au cours de l'expansion de l'Univers, donc une dynamique plus complexe est nécessaire pour éviter sa dilution. Différents modèles ont été proposés dans la littérature, avec un potentiel V(Aμ2) pour le vecteur Aμ, des couplages non-minimaux à la gravitation, R f(Aμ2) voire R f(Fμν2), ou encore des termes cinétiques non-linéaires f(Fμν2) étendant aux vecteurs les modèles scalaires dits de "k-essence".
Le but de notre article est en premier lieu d'étudier la cohérence mathématique de telles théories des champs, c'est-à-dire si leur problème de Cauchy est bien posé (en analysant l'hyperbolicité de leurs équations des champs) et si leur hamiltonien est borné inférieurement (pour assurer leur stabilité). Nous rappelons que dans la classe des termes cinétiques quadratiques, un mode d'hélicité 0 et d'énergie négative est génériquement excité, et que seul le lagrangien de Maxwell (ou Proca) proportionnel à Fμν2 permet de l'éviter. Nous montrons ensuite que la classe des fonctions f(Fμν2) non-linéaires conduit nécessairement à des équations non-hyperboliques pour certaines conditions initiales, et que pour éviter cette difficulté, il est nécessaire de les généraliser à des fonctions f(F2, FF̃), où F̃ désigne le dual du tenseur de Faraday. Mais notre étude de l'évolution cosmologique de cette classe de modèles montre de toutes façons que la valeur de fond du vecteur tend vers zéro dans un Univers en expansion. Nous restreignant alors à un terme cinétique usuel Fμν2, nous étudions les conséquences de couplages non-minimaux du vecteur à la courbure. Une subtile diagonalisation des termes cinétiques nous permet de prouver que les couplages du type R f(A2) conduisent toujours à des modèles instables, car leur densité de hamiltonien n'est pas bornée inférieurement. Le cas des couplages R f(F2) est à la fois plus complexe, à cause du fort mélange des degrés de liberté de spin 1 et 2, et plus simple car les équations de champs sont du troisième ordre. Non seulement nous donnons des arguments indiquant la probable instabilité de tels modèles, mais nous savons aussi qu'ils ne contiennent pas seulement le graviton et le vecteur que nous désirions au départ (car les champs et leurs premières dérivées temporelles données sur une surface de genre espace ne suffisent pas pour prédire leur évolution temporelle). Pour finir, nous montrons que les couplages non-minimaux issus de la réduction dimensionnelle d'invariants de Gauss-Bonnet-Lovelock sont très prometteurs pour la cosmologie. Nous rappelons en effet qu'ils conduisent à des équations des champs d'ordre 2 (malgré la présence de dérivées d'ordres supérieurs dans l'action), évitant ainsi l'instabilité générique des théories d'ordres supérieurs à 2. En raison de leur complexité, nous n'analysons pas leur problème de Cauchy ni leur stabilité comme nous l'avons fait pour les précédents modèles, mais nous soulignons qu'ils peuvent conduire à une évolution cosmologique dans laquelle la valeur de fond du vecteur est constante voire croissante. Cette classe de couplages non-minimaux est donc a priori la plus saine si les données observationnelles sont en faveur d'une légère anisotropie de l'Univers. Mes travaux récents sur les théories de galiléons et de Horndeski généralisées peuvent être considérés commes des suites naturelles de cette étude de champs vectoriels couplés non-minimalement à la courbure (cf. le chapitre VIII ci-dessous).
Les sources d'ondes gravitationnelles les plus prometteuses pour les interféromètres LIGO et VIRGO sont les systèmes binaires très rapides, peu de temps avant leur coalescence. Comme des milliers d'orbites seront observées dans la bande passante de ces détecteurs, il est nécessaire de décrire le mouvement spiralant des deux corps avec une grande précision, à savoir jusqu'à l'ordre "3.5 PN", c'est-à-dire 1/c7 au delà des prédictions newtoniennes. Il se trouve que l'ordre 3.5 PN lui-même se traite assez facilement, mais que de sérieuses difficultés mathématiques concernent l'ordre 3PN (1/c6). En effet, si les deux corps sont schématisés par des particules ponctuelles (distributions de Dirac), des singularités se manifestent dans les calculs, et la méthode de régularisation d'Hadamard ne suffit plus pour les résoudre à cet ordre 3PN. Il est donc nécessaire soit de modéliser la structure interne de corps étendus, soit d'employer une autre technique de régularisation.
Ma collaboration avec Luc Blanchet sur ce sujet a commencé dès mon séjour au DARC en 2000–2001. Les équations du mouvement d'un système binaire à l'ordre 3PN étaient à l'époque connues à un coefficient numérique près, que la régularisation d'Hadamard ne permettait pas de déterminer. Par la suite, Damour, Jaranowski et Schäfer ont pu le calculer en employant la régularisation dimensionnelle en jauge ADM (Arnowitt-Deser-Misner). En collaboration avec Luc Blanchet et son étudiant en thèse Olivier Poujade, nous avons cherché à confirmer cette valeur en modélisant les corps de la façon la plus réaliste possible, comme des objets étendus dont l'équation d'état peut être quelconque. Cette méthode a nécessité le développement de programmes algébriques très complexes, et la taille des calculs était considérable. Nous avons obtenu l'énergie totale de ce système de deux corps étendus à l'ordre 3PN, mais nous n'avons pas su trouver la jauge dans laquelle le résultat se simplifiait assez. [Il s'agit plus précisément d'une redéfinition des trajectoires des points matériels constituant les corps étendus.] Essentiellement à cause de sa taille inhumaine, nous n'avons donc pas achevé ce travail, malgré plusieurs résultats partiels intéressants. à l'ordre 1PN (1/c2), nous avons montré que l'énergie du système de corps étendus coïncide bien avec celle de deux corps ponctuels, après changement de jauge et surtout renormalisation des masses. En effet, une contribution à l'énergie totale est l'énergie de liaison gravitationnelle des corps étendus, qui diverge formellement en 1/R quand on fait tendre le rayon R des corps vers zéro. Il faut donc tenir compte de tels termes dans la définition de leurs masses. À l'ordre 2PN (1/c4), notre résultat se réduit aussi à celui obtenu avec des corps ponctuels, après changement de jauge et élimination de tous les termes divergents en 1/R. La renormalisation des masses permettant d'éliminer convenablement ces termes divergents n'a toutefois pas été démontrée. À l'ordre 3PN (1/c6), notre résultat était presque identique à celui des masses ponctuelles (toujours après changement de jauge et élimination des termes divergents), mais il nous restait quelques termes (sur des centaines !) dépendant de la structure interne des corps. La compatibilité des nombreux termes corrects suggère que notre calcul était cohérent, mais nous ne l'avons pas achevé. Nous nous sommes en effet consacrés à une autre méthode de calcul qui a heureusement porté tous ses fruits.
Durant les années 2003–05, en collaboration avec Luc Blanchet et Thibault Damour, nous avons repris la technique de la régularisation dimensionnelle, mais en jauge harmonique (au lieu de la jauge ADM employée par Damour, Jaranowski et Schäfer). Cette jauge permet en effet de calculer le développement multipolaire des ondes gravitationnelles émises, alors que la jauge ADM ne fournit de façon élégante que les équations du mouvement. Nous avons généralisé les nombreux calculs post-newtoniens de la littérature en dimension d+1 quelconque (équations des champs et des géodésiques, calcul des potentiels définissant la métrique à l'aide d'intégrales de Poisson ou d'intégrales retardées). Les singularités liées au choix de particules ponctuelles se manifestent alors comme des pôles proportionnels à 1/(d–3). Le résultat central de notre travail est que ces pôles peuvent être éliminés par une renormalisation des lignes d'univers des deux particules : les trajectoires nues intervenant dans leur action initiale ne sont pas observables, et seules les trajectoires renormalisées, sans divergences, ont un sens physique. Ces renormalisations des lignes d'univers reviennent aussi à attribuer à chaque particule un dipôle infini en plus de son monopôle de masse, afin de compenser le dipôle créé par son propre champ gravitationnel en présence d'un deuxième corps qui l'accélère. Après renormalisation, les résultats restent finis en dimension d tendant vers 3, et nous terminons ainsi le calcul des équations du mouvement d'un système binaire à l'ordre 3PN : le dernier coefficient que la régularisation d'Hadamard n'avait pas permis de déterminer est désormais connu sans la moindre ambiguïté. Le long article [29] détaille notre technique de calcul, certes plus efficace que celle des corps étendus, mais néanmoins fort subtile.
Ces équations du mouvement ne sont qu'un premier pas pour calculer les ondes gravitationnelles émises par un tel système binaire spiralant. Les méthodes classiques utilisant la régularisation d'Hadamard en dimension 3 avaient jusque là permis leur calcul, mais trois coefficients (sur des centaines) restaient indéterminés. Or leur détermination était nécessaire pour prédire des patrons d'ondes suffisamment précis pour l'analyse des signaux détectés par LIGO et VIRGO. Notre second travail, cette fois en collaboration avec Bala Iyer en plus de Luc Blanchet et Thibault Damour [31, 34], a donc été le calcul de ces ondes gravitationnelles en régularisation dimensionnelle. Grâce à notre choix de la jauge harmonique, ce travail était désormais abordable. Il nous a de nouveau fallu généraliser les résultats post-newtoniens passés en dimension d+1 quelconque, et notamment définir correctement les moments multipolaires. Certaines subtilités sont liées au fait que la source du champ gravitationnel n'est pas à support compact, car les ondes gravitationnelles emplissent tout l'espace et sont elles-mêmes des sources (non-linéarité de la théorie d'Einstein). Cela conduit à des divergences infrarouges, en plus des ultraviolettes intervenant au voisinage des corps ponctuels. En régularisation dimensionnelle, ces deux types de divergences sont subtilement mêlés. Comme dans le cas des équations du mouvement, nous avons trouvé que les singularités se manifestent comme des pôles proportionnels à 1/(d–3). Notre résultat crucial est que la même renormalisation des lignes d'univers que pour les équations du mouvement suffit pour les éliminer. Nous aboutissons donc à une expression finie et sans aucune ambiguïté. Par ailleurs, la valeur numérique d'une combinaison de paramètres intervenant pour les orbites circulaires indique que la série post-newtonienne converge assez rapidement. Ce travail achève donc le calcul des formes d'ondes gravitationnelles, nécessaires pour l'analyse de données des interféromètres LIGO et VIRGO. Il est l'aboutissement d'années d'efforts de plusieurs chercheurs, et peut être considéré comme le couronnement des travaux sur les développements post-newtoniens. En raison de l'importance de ces résultats, nous les avons rapidement publiés dans une lettre [31], mais les détails de la méthode, des calculs et de nos multiples vérifications ont été exposés par la suite dans l'article [34].
La théorie purement scalaire de Nordström, proposée deux ans avant la relativité générale, est relativiste et reproduit la loi de Newton au premier ordre, mais elle est incompatible avec les tests classiques dans le système solaire à l'ordre post-newtonien. Elle reste néanmoins un excellent modèle simplifié pour étudier la gravitation, et notamment son difficile problème à deux corps en présence de rayonnement gravitationnel. Cette théorie présente en outre l'avantage de conserver beaucoup de points communs avec la relativité générale : il s'agit d'une théorie des champs cohérente, sans fantômes ni référentiel privilégié, son rayonnement gravitationnel commence à l'ordre 1/c5, et surtout elle respecte exactement le principe d'équivalence fort. Pour décrire le mouvement orbital d'un corps, il est donc possible de négliger sa structure interne et de le schématiser comme une particule ponctuelle de masse constante (cela n'est justifié que pour les théories d'Einstein et de Nordström). Le grand avantage par rapport à la relativité générale est que l'on peut trouver une solution exacte du champ gravitationnel (scalaire), quelle que soit la configuration de telles particules ponctuelles. Leurs équations du mouvement peuvent alors aussi être écrites de façon exacte, en tenant compte de leurs auto-interactions ("self-forces") et des renormalisations qu'elles imposent. Seule la dernière étape présente de réelles difficultés : obtenir une solution de ces équations du mouvement. En collaboration avec mon étudiant en thèse Jean-Philippe Bruneton, nous nous sommes concentrés sur le mouvement à deux corps. En supprimant tout d'abord le rayonnement gravitationnel, c'est-à-dire en considérant la fonction de Green retardée+avancée, nous avons obtenu une solution exacte pour le mouvement circulaire (tenant donc compte de tous les ordres en puissances de v/c, y compris un pôle en v → c dû à un effet de relativité restreinte). Le calcul du hamiltonien nous permet de définir la notion de dernière orbite circulaire (ICO), comme en relativité générale, et nous obtenons un résultat surprenant : cette ICO n'existe pas de façon exacte, bien que la solution tronquée aux ordres post-newtoniens successifs en prédise parfois une et que les approximations successives donnent l'impression de converger. Cela ne met pas directement en doute les calculs analogues en relativité générale, car cette absence d'ICO est liée aux propriétés de la théorie de Nordström (notamment l'absence de trous noirs), mais ce résultat illustre néanmoins que des solutions non-perturbatives peuvent parfois se comporter très différemment de leurs développements limités. En prenant cette solution circulaire comme approximation d'ordre zéro, nous avons ensuite cherché une solution spiralante réaliste, tenant compte du rayonnement gravitationnel (avec la fonction de Green retardée). Nous avons élaboré une méthode itérative qui converge en puissances de 1/c5 — au lieu de 1/c dans les méthodes post-newtoniennes habituelles. Outre cette convergence accélérée, chaque ordre contient aussi des informations non-perturbatives quand v → c. La première itération, appliquée à la solution circulaire de départ, fournit déjà la réaction de rayonnement d'ordre 4.5 PN (proportionnelle à 1/c14), et les ordres suivants peuvent être écrits de manière constructive. Ces résultats éclairent non seulement certains aspects non-perturbatifs de la gravitation relativiste, mais peuvent aussi être utiles pour tester les codes de gravitation numérique, pour lesquels la théorie de Nordström est un intermédiaire idéal entre les (trop simples) modèles newtoniens et les (trop longues) simulations complètement relativistes. Jean-Philippe Bruneton a présenté nos principaux résultats dans plusieurs séminaires & conférences (certaines ayant donné lieu à des actes).
Le spectre d'absorption d'un champ scalaire par un trou noir présente des oscillations autour d'une valeur moyenne, la section géométrique de sa sphère de photons. Ces oscillations sont coûteuses à calculer numériquement par la méthode standard, consistant à décomposer l'onde plane entrante en harmoniques sphériques. En collaboration avec Y. Décanini et A. Folacci [43], nous avons montré que ces oscillations peuvent être obtenues très précisément à partir de résidus calculés aux pôles de Regge, c'est-à-dire en prolongeant les indices de ces ondes partielles dans le plan complexe. Dans la limite des hautes fréquences, nous obtenons même une très simple expression analytique, qui garde une forme universelle pour tous les trous noirs sphériques (chargés ou non, gravitationnels ou acoustiques) en dimension quelconque. Elle fait intervenir les caractéristiques (période orbitale et exposant de Lyapounov) des géodésiques sur la sphère de photons.
Les travaux présentés dans ce chapitre ont été menés dans le cadre de deux projets successifs financés par l'ANR et réunissant des chercheurs de l'IAP et d'APC : "MODGRAV" (Modifications à grande distance de l'interaction gravitationnelle) en 2006–09 ; puis "THALES" (Théories alternatives pour la matière et l'énergie sombres) en 2010–14.
Les courbes de rotation des galaxies et des amas sont en général expliquées par la présence de matière noire, et autant les observations que les simulations numériques confirment de jour en jour le bien fondé de cette hypothèse. Toutefois, il reste théoriquement possible qu'elles soient plutôt la manifestation d'une modification de la loi de Newton à grande distance, c'est-à-dire à petite accélération. M. Milgrom a ainsi proposé en 1983 un modèle phénoménologique, baptisé MOND (Modified Newtonian Dynamics), qui reproduit remarquablement bien de nombreuses observations astrophysiques. Durant près de 25 ans, diverses théories relativistes de la gravitation ont été imaginées pour prédire une telle dynamique.
En collaboration avec mon étudiant Jean-Philippe Bruneton (qui a soutenu sa thèse fin 2007 avec mention très honorable), j'ai effectué en 2006–07 une étude critique et détaillée de ces diverses théories. Dans le long article [36], nous soulignons leurs succès et leurs problèmes, notamment que beaucoup d'entre elles ne sont pas cohérentes en tant que théories des champs, soit parce qu'elles ne peuvent provenir d'un principe variationnel, soit parce que leur hamiltonien n'est pas borné inférieurement. Nous mettons aussi en évidence de nouvelles difficultés qui n'avaient pas été discutées dans la littérature, en particulier le fait qu'un ajustement fin de certaines fonctions est nécessaire pour ne pas être incompatibles avec les tests post-newtoniens dans le système solaire ou les données des pulsars binaires. En revanche, nous montrons que plusieurs théorèmes d'impossibilité de la littérature sont fondés sur des hypothèses pas forcément nécessaires, donc que l'espace des théories possibles est a priori plus grand. Nous soulignons en particulier que la propagation de champs à une vitesse supérieure à celle de la lumière n'est pas toujours un problème pour la causalité, à condition que certaines propriétés mathématiques restent satisfaites par les équations de ces champs. Les modèles de "k-essence" (dans lesquels l'action contient une fonction non-linéaire du terme cinétique du champ scalaire) sont donc de bons candidats pour reproduire la phénoménologie MOND. Nous en examinons une nouvelle classe, pour lesquelles les équations des champs sont particulièrement simples dans le vide (relativité générale ou Brans-Dicke), les effets MONDiens étant dus à un couplage plus complexe de la matière aux champs de gravitation. Toutefois, notre analyse des équations des champs à l'intérieur de la matière (problème crucial que la littérature oubliait de traiter) révèle qu'elles ne restent pas hyperboliques dans toutes les situations, et donc que ces modèles sont incohérents en tant que théories des champs. Mais au passage, nous trouvons que ce cadre théorique fournit un modèle stable et au problème de Cauchy bien posé, capable de reproduire l'anomalie des sondes Pioneer (accélération légèrement trop grande vers le Soleil, à l'époque encore inexpliquée) sans modifier les autres prédictions testées de la relativité générale. En ce qui concerne la phénoménologie MOND elle-même, notre conclusion est que tous les modèles proposés (y compris les nouveaux que nous avons explorés) présentent de sérieuses difficultés, soit au niveau expérimental, soit au niveau de la cohérence mathématique, et qu'ils sont en outre toujours ajustés finement d'une façon fort peu naturelle. Certains modèles sont toutefois plus prometteurs que d'autres et nous indiquons dans quelles directions il faudrait les améliorer.
L'un des modèles les plus prometteurs, parmi ceux étudiés ci-dessus, est celui proposé par J. Bekenstein, appelé "TeVeS" (tenseur-vecteur-scalaire). Toutefois, l'une des fonctions qui le définit doit être ajustée finement pour être compatible avec les tests de la gravitation effectués dans le système solaire et les pulsars binaires (cf. le chapitre IV.6 ci-dessus), tout en conservant un hamiltonien borné inférieurement et un problème de Cauchy bien posé. Dans l'article [44] en collaboration avec E. Babichev et C. Deffayet, nous avons montré que cette théorie TeVeS peut être considérablement simplifiée grâce à un couplage particulier du champ scalaire à la courbure de l'espace-temps, issu des théories dites de "galiléons" généralisés (cf. le chapitre VIII ci-dessous). Bien que fortement non-linéaire, ce couplage conduit à des équations des champs ne contenant que des dérivées d'ordre ≤ 2, et évite ainsi les instabilités d'Ostrogradski associées aux dérivées d'ordres supérieurs. Il permet d'effacer les effets du champ scalaire à petite distance, de manière similaire à l'effet Vainshtein se produisant en gravité massive. La théorie devient ainsi facilement compatible avec les tests du système solaire et des pulsars binaires, sans nécessiter d'ajustement fin de fonction ni même devoir spécifier la dynamique du champ vectoriel.
Dans l'article [45] en collaboration avec C. Deffayet et R. Woodard, nous avons exploré une autre façon de reproduire la phénoménologie de MOND, dans une théorie non-locale de la gravitation, c'est-à-dire dépendant de l'ensemble du cône passé de chaque événement. Nous ne présupposons pas que la théorie fondamentale sous-jacente est elle-même non-locale, mais de telles extensions non-locales de la relativité générale sont engendrées par les corrections quantiques infrarouges, qui deviennent non-perturbativement fortes durant la phase d'inflation cosmologique primordiale. Autrement dit, la phénoménologie de MOND serait ici causée par la polarisation gravitationnelle du vide des très nombreux gravitons infrarouges créés durant l'inflation. Comme nous ne savons pas prédire ces interactions non-locales à partir de calculs de gravitation quantique, nous avons adopté un point de vue phénoménologique : est-il possible de construire une telle théorie reproduisant MOND à grande distance, compatible avec les observations de lentilles gravitationnelles, tendant vers la relativité générale à petite distance, et ne dépendant (non-localement mais causalement) que d'une métrique gμν, sans introduire aucun autre champ ? Nous avons montré que la réponse est positive, et même qu'il est nécessaire que la théorie soit non-locale, c'est-à-dire qu'une théorie locale purement métrique ne peut pas reproduire MOND.
Ce travail se concentrait sur la limite des champs faibles dans une géométrie statique à symétrie sphérique. En 2014 [49], nous avons su écrire les équations des champs complètes de ce modèle. C'est un travail subtil précisément à cause de sa nature non-locale. Notre technique a consisté à le transformer en théorie locale grâce à l'introduction de champs scalaires temporaires, dont nous gelons in fine la dynamique en imposant des conditions initiales nulles. La causalité de nos équations est garantie par le fait que nous utilisons partout des fonctions de Green retardées.
Nous avons finalement particularisé nos équations à la cosmologie, et plus précisément à un univers homogène, isotrope et sans courbure spatiale. Nous avons aussi explicitement écrit les intégrales temporelles permettant de résoudre les équations non-locales, et expliqué la procédure à suivre pour ajuster les fonctions libres du modèle afin de reproduire une cosmologie compatible avec les différentes phases de son expansion — avec donc le même état d'esprit que dans les chapitres V.1 et V.2 ci-dessus. Ce travail explicite de reconstruction a été effectué par la suite par R. Woodard et plusieurs étudiants (confirmant d'ailleurs une subtilité que j'avais remarquée dès la rédaction de [49] : il est impossible de reproduire exactement la cosmologie standard, car cela impliquerait qu'une fonction doit être bi-valuée ; mais une reconstruction approchée, compatible avec les observations, reste néanmoins possible).
Pour finir, nous avons généralisé ce modèle au cas plus complexe, mais probablement plus réaliste, où la constante a0 de MOND (qui a la dimension d'une accélération) est remplacée par une variable évoluant au cours de l'expansion cosmologique. Ici encore, notre technique traduisant temporairement le modèle sous forme locale, en introduisant des champs scalaires dont la dynamique est gelée in fine, a permis d'écrire les équations des champs générales de façon explicite.
Les théories dites de "galiléons" ont été très étudiées ces dernières années, aussi bien du point de vue de leurs prédictions observationnelles que de leurs symétries, leurs propriétés quantiques ou leur cohérence mathématique. Elles remontent en fait aux travaux de Horndeski en 1974, puis aux recherches plus mathématiques de Fairlie, Govaerts et Morozov en 1992, mais c'est seulement depuis Nicolis, Rattazzi et Trincherini en 2009 qu'elles ont autant attiré l'attention des théoriciens des champs et de la gravitation (en raison des intéressantes cosmologies auxquelles elles conduisent, notamment l'existence d'une phase d'expansion accélérée de l'Univers sans introduire d'énergie noire ni de constante cosmologique). Il s'agit de théories tenseur-scalaire dont l'action dépend non-linéairement des dérivées secondes des champs, mais dont les équations du mouvement ne font pourtant intervenir aucune dérivée troisième ou supérieure. L'exemple le plus simple (au delà du terme cinétique standard d'un champ scalaire, ∂μφ∂μφ) est obtenu dans la limite de découplage du modèle branaire de Dvali, Gabadadze et Porrati : l'action contient un terme (∂μφ)2 ⧠φ, mais les dérivées troisièmes auxquelles on s'attendrait dans les équations de champs s'annulent exactement, pour ne donner qu'une combinaison (∇μ∂νφ)2–(⧠φ)2, certes non linéaire mais ne dépendant que de dérivées secondes.
En collaboration avec C. Deffayet et A. Vikman [38], nous avons analysé le comportement de tels modèles en espace courbe de dimension 4, et avons montré que les équations de champs (de la métrique et du champ scalaire) deviennent alors d'ordre 3, conduisant à de probables instabilités dues à l'excitation de degrés de liberté supplémentaires. Pour retrouver des équations d'ordre (au plus) 2, nous montrons qu'il faut et il suffit de coupler non-minimalement le scalaire à la courbure, d'une façon unique que nous établissons, et nous calculons ces équations explicitement, y compris le volumineux tenseur énergie-impulsion du champ scalaire. Comme elles font maintenant intervenir des dérivées premières de ce scalaire (en plus de ses dérivées secondes), la symétrie originelle des modèles de galiléons est donc perdue en espace courbe, mais leur ordre 2 montre qu'il s'agit d'une nouvelle classe de théories tenseur-scalaire dont la phénoménologie mérite d'être étudiée. Dans ce travail, nous avons en fait redémontré les résultats de 1974 de Horndeski, que la communauté scientifique avait oubliés. Les galiléons de Nicolis, Rattazzi et Trincherini (2009) en étaient eux-mêmes la restriction à un espace-temps plat.
Toujours en collaboration avec C. Deffayet, mais cette fois aussi avec S. Deser, nous avons généralisé ce travail dans [40] au cas d'un espace courbe de dimension quelconque. Nous montrons tout d'abord que la classe des modèles de galiléons se réécrit d'une manière particulièrement compacte en espace plat, en termes du tenseur complètement antisymétrique de Levi-Civita (d'une manière analogue aux invariants topologiques de Gauss-Bonnet-Lovelock). Cette écriture, combinée à des notations multi-indices, nous permet alors de calculer les uniques couplages non-minimaux à la courbure qui éliminent les dérivées d'ordres supérieurs, à la fois dans l'équation du champ scalaire et dans son tenseur énergie-impulsion. Ces couplages font intervenir des produits de dérivées premières & secondes du champ scalaire et de plusieurs tenseurs de Riemann. Notre analyse traite simultanément tous les modèles de galiléons possibles en dimension quelconque. Outre l'intérêt des modèles de dimension 4 en cosmologie, comme rappelée ci-dessus, la réduction dimensionnelle à la Kaluza-Klein des nouveaux modèles possibles en dimensions supérieures peut également conduire à une intéressante phénoménologie (cf. le chapitre V.3).
Finalement, nous avons montré dans [42] que cette notion de galiléon généralisé pouvait aussi être définie, en espace courbe de dimension arbitraire, pour des p-formes de degrés quelconques, y compris couplées les unes aux autres. Nos résultats fournissent ainsi une vaste classe de théories dont les équations dépendent de dérivées d'ordres ≤ 2. Notons que nos trois articles [38, 40, 42] ont un fort taux de citation.
L'absence de dérivées d'ordres supérieurs évite les instabilités génériques dues aux fantômes d'Ostrogradski, mais elle ne garantit en rien que ces théories de galiléons sont stables. Il est d'ailleurs facile de montrer qu'en espace-temps plat, le hamiltonien de ces théories n'est pas borné inférieurement, donc qu'il faut les considérer comme des théories effectives au voisinage de fonds spécifiques. L'analyse de leur stabilité en présence de gravitation est bien plus difficile, en raison du mélange des termes cinétiques du graviton et du champ scalaire. Il est alors nécessaire d'étudier le comportement de perturbations au voisinage d'un fond particulier. Mon travail de 2013 en collaboration avec E. Babichev [48] a consisté à analyser la stabilité du modèle cubique (le plus simple mentionné ci-dessus, auquel on additionne aussi un terme cinétique standard) dans une situation assez réaliste : au voisinage d'un corps matériel sphérique plongé soit dans un univers en expansion, soit dans un espace-temps asymptotiquement plat. L'expansion cosmologique que nous avons considérée n'est pas due à une constante cosmologique, que nous présupposons nulle, mais au galiléon lui-même, qui engendre une solution de de Sitter "auto-accélérée".
La première surprise phénoménologique est qu'une évolution temporelle cosmologique du galiléon induit un couplage supplémentaire de ce champ scalaire à la matière, causé par le mélange des termes cinétiques des spins 0 et 2. Ce couplage est génériquement d'ordre 1, c'est-à-dire similaire au couplage entre matière et gravitons. Le profil du champ scalaire n'est donc pas trivial au voisinage d'un corps massif, même si le couplage matière-galiléon nu est choisi strictement nul dans l'action.
La deuxième surprise est que la solution locale à symétrie sphérique dépend de façon cruciale des conditions asymptotiques : selon que l'univers se comporte comme l'espace de Minkowski ou celui de de Sitter à grande distance, le champ scalaire correspond à deux branches différentes de solutions locales.
Pour analyser la stabilité, nous avons diagonalisé les termes cinétiques des perturbations au voisinage du fond choisi. Nous trouvons que les gravitons sont toujours d'énergie positive, mais que le champ scalaire se propage dans une métrique effective dépendant du fond. Nous avons donc étudié la signature de cette métrique effective dans tous les régimes du modèle : à très grande distance de la source matérielle ; proche de cette source, où l'effet Vainshtein réduit les déviations observables causées pas le champ scalaire, mais où la stabilité de ce champ reste néanmoins cruciale ; et finalement à l'intérieur du corps matériel lui-même, où le tenseur de Ricci non nul engendre de nouveaux couplages matière-scalaire à prendre en compte.
Nous avons démontré que tous ces régimes sont stables et ont un problème de Cauchy bien posé, bien que ce ne soit vraiment pas évident a priori. En particulier, le fait que deux branches de solutions locales correspondent aux différentes conditions asymptotiques s'est avéré fondamental. En effet, la mauvaise branche (ne se raccordant pas correctement aux conditions asymptotiques) conduit au contraire à des perturbations scalaires d'énergie cinétique négative (fantômes). C'est donc la cohérence globale de la solution qui garantit la stabilité du modèle dans tous ces régimes.
Notre analyse de la stabilité à l'intérieur du corps matériel a apporté une troisième surprise : toujours à cause du mélange des termes cinétiques des spins 0 et 2, une évolution temporelle cosmologique du galiléon induit une force de friction qui amortit efficacement toute perturbation scalaire dans la matière. Paradoxalement, le comportement de l'Univers à grande distance influence donc de façon significative la physique locale. Il était important de démontrer qu'il s'agit d'une friction, et non d'une amplification des perturbations scalaires, sinon cela aurait signifié qu'il existe un autre type d'instabilité, tachyonique malgré l'absence de fantômes soulignée ci-dessus.
En conclusion, le modèle de galiléon cubique est toujours stable dans les fonds que nous avons considérés, à condition de choisir la branche de solution locale compatible avec le comportement asymptotique. Contrairement à la relativité générale, qui possède un "principe d'effacement", la physique locale est ici intimement liée à ce qui se passe à grande distance, autant pour l'absence de fantômes que pour l'amortissement des perturbations scalaires à l'intérieur de la matière.
Au chapitre VII.2 ci-dessus, nous avons vu que les effets d'un champ scalaire peuvent être écrantés à courtes distances grâce à une généralisation de l'effet Vainshtein ("k-mouflage") [44]. On s'attend alors à ce qu'aucune déviation de la relativité générale ne puisse être observable dans le système solaire. Toutefois, nous montrons dans [46] qu'un effet cosmologique n'est paradoxalement pas supprimé par ce mécanisme, dans les théories tenseur-scalaire ne dépendant que du gradient de ce champ : la variation temporelle de la constante de gravitation. Cela réduit donc l'espace des théories envisageables. Grâce au couplage non conforme de la matière au champ scalaire, le modèle MONDien décrit au chapitre VII.2 ne présente pas cette difficulté.
L'article [50] est le résultat d'un travail fort difficile, qui a duré plus d'un an. Nos travaux [38, 40, 42] de 2009–10 avaient montré comment éviter la présence de dérivées d'ordres supérieurs à 2 dans les équations de champs des théories de galiléons généralisés, en espace courbe. Pour cela, il était nécessaire d'introduire de très précis couplages non-minimaux à la courbure, comme rappelé au chapitre VIII.1 ci-dessus. Ces équations différentielles d'ordre 2 (ou moins) garantissaient l'absence de fantômes d'Ostrogradski. Mais en 2014, Gleyzes, Langlois, Piazza et Vernizzi ont remarqué, dans un contexte cosmologique, que les coefficients précis de ces couplages non-minimaux pouvaient être quelconques sans pour autant exciter de degré de liberté supplémentaire. En particulier, ces coefficients pouvaient être choisis nuls (absence de couplages non-minimaux à la courbure), et la théorie semblait pourtant ne compter que trois degrés de liberté : les deux polarisations du graviton de spin 2 sans masse, et un unique degré de liberté scalaire. Leur résultat était d'autant plus paradoxal que les équations de champs contiennent des dérivées temporelles troisièmes du scalaire et de la métrique, dans ce cas. On s'attend donc à ce qu'il soit nécessaire de spécifier davantage de conditions initiales (que les champs et leur dérivée temporelle première) sur une surface de Cauchy, ce qui est le signe d'au moins un degré de liberté en plus, génériquement d'énergie négative. Ces quatre auteurs (ainsi que Lin, Mukohyama, Namba et Saitou) ont ensuite publié plusieurs arguments en faveur de leur étonnant résultat, mais aucun n'a réellement convaincu la communauté scientifique internationale. Leur calcul principal était une analyse hamiltonienne, mais effectuée après avoir partiellement fixé la jauge — à savoir la jauge unitaire, dans laquelle le champ scalaire est choisi comme coordonnée temporelle. Or, il est possible dans des cas plus simples de montrer que le comptage des degrés de liberté peut être totalement erroné si l'on part d'une action fixée de jauge. Avec C. Deffayet et D. Steer, nous nous sommes aussi rapidement rendu compte que cette jauge unitaire élimine depuis le début le seul terme responsable de l'apparition de dérivées temporelles troisièmes dans les équations de champs. Il n'est donc pas très étonnant que Gleyzes et al. n'aient pas trouvé de degré de liberté supplémentaire. Par la suite, en en discutant avec D. Langlois et K. Noui après la publication de notre article [50], j'ai en fait construit un modèle-jouet contenant bel et bien un fantôme d'Ostrogradski, mais qu'on ne voit pas si l'on travaille en jauge unitaire. Cet exemple souligne que nos doutes sur les arguments initiaux de Gleyzes et al. étaient justifiés. Avec C. Deffayet et D. Steer, nous avions aussi compris qu'un autre argument de Gleyzes et al. ne prouvait rien : ils se servaient d'une équation de champ contenant une dérivée temporelle troisième (∂t3φ = champs dérivés au plus deux fois par rapport au temps) afin de remplacer partout ailleurs cette dérivée troisième par des dérivées d'ordres temporels au plus 2. Mais ils ne pouvaient bien évidemment pas effectuer ce remplacement dans cette équation-même, sinon l'on obtient la trivialité 0 = 0, et l'une des équations de champs est tout simplement perdue. Contrairement à ce que Gleyzes et al. prétendaient, leur procédure ne changeait donc rien à l'ordre global de l'ensemble des équations. Il restait toutefois possible que leur conclusion soit néanmoins correcte, c'est-à-dire que cette vaste classe de théories ne contienne qu'un seul degré de liberté scalaire malgré des équations d'ordre 3.
Afin de trancher cette question, nous avons donc entrepris dans [50] une analyse hamiltonienne complète, sans fixer la jauge. Précisément à cause des termes engendrant des dérivées temporelles troisièmes, c'est un travail d'une très grande complexité technique comparé au calcul en jauge unitaire. Nous nous sommes donc concentrés sur le modèle le plus simple engendrant de telles dérivées troisièmes : le galiléon quartique. Introduisant plusieurs tenseurs auxiliaires nous permettant d'inverser les relations entre variables lagrangiennes et moment canoniques de l'analyse hamiltonienne, nous avons calculé le hamiltonien puis les nombreuses contraintes que la théorie satisfait. La plus grande difficulté de ce travail est alors de déterminer quelles sont les contraintes de première classe, c'est-à-dire les combinaisons linéaires de contraintes qui commutent avec toutes les autres. En effet, ces contraintes de première classe sont associées à des symétries de jauge, donc éliminent deux fois plus de degrés de liberté que les contraintes de seconde classe. Quatre d'entre elles, ainsi que les quatre contraintes secondaires que leur conservation implique, sont bien sûr associées à l'invariance sous difféomorphismes de la théorie. Après les avoir identifiées, il nous restait à déterminer si toutes les autres, associées au champ scalaire et à nos tenseurs auxiliaires, étaient bien de seconde classe. De longs et très volumineux calculs l'ont confirmé, mais avec une belle subtilité. Toutes les contraintes primaires (de seconde classe) engendrent en effet des contraintes secondaires (également de seconde classe), mais l'une d'entre elles engendre aussi une contrainte tertiaire et même une quaternaire ! Ces calculs sont si complexes que nous n'avons pas écrit explicitement ces contraintes tertiaire et quaternaire, mais notre raisonnement suffit pour prouver leur existence. In fine, cette existence de deux contraintes supplémentaires est justement responsable de la réponse que nous cherchions : ce modèle ne contient bien qu'un seul degré de liberté scalaire, et non deux comme la présence de dérivées temporelles troisièmes dans les équations le laissait craindre. Donc le résultat de Gleyzes et al. est finalement correct, bien que leur démonstration ne le prouvait pas vraiment.
Pour compléter ce résultat solide obtenu dans le cas particulier du galiléon quartique, nous avons ensuite cherché à corriger le second argument erroné de Gleyzes et al., rappelé ci-dessus. Au lieu de nous servir comme eux d'une équation d'ordre 3 temporel, nous avons utilisé des équations d'ordre 2. Nous avons en effet identifié une combinaison linéaire d'équations de champs nous permettant d'exprimer la dérivée seconde temporelle du champ scalaire, ∂t2φ, en termes de dérivées temporelles au plus premières. Nous conservons bien sûr cette combinaison inchangée dans notre système d'équations, mais nous avons le droit de nous servir de sa dérivée temporelle pour simplifier les autres. En effet, elle nous permet de remplacer toutes les dérivées temporelles troisièmes du champ scalaire par des dérivées temporelles au plus secondes. Nous avons aussi identifié une autre combinaison linéaire d'équations de champs, permettant d'exprimer une certaine contraction de ∂t2gij (dérivée temporelle seconde de la métrique spatiale) en termes de dérivées temporelles au plus premières. La dérivée temporelle de cette combinaison nous permet donc d'éliminer une contraction de dérivées temporelles troisièmes de la métrique, en termes de champs dérivés au plus deux fois par rapport au temps. Il se trouve que les seules ∂t3gμν intervenant dans les équations de champs prennent précisément la forme de cette contraction. Par conséquent, notre procédure permet de supprimer toutes les dérivées temporelles troisièmes (il n'y en a pas d'ordres supérieurs), mais sans perdre la moindre équation. Cela semble donc confirmer que la donnée des champs et de leur première dérivée temporelle sur une surface de Cauchy suffit pour prédire sans ambiguïté leur évolution, et donc pourquoi il n'y a qu'un seul degré de liberté scalaire. Toutefois, notre procédure brise l'invariance de Lorentz explicite, donc nous soulignons qu'il ne s'agit pas d'une preuve, contrairement à notre précédente analyse hamiltonienne complète. Il s'agit juste d'une version correcte du second argument employé par Gleyzes et al. Notons que notre procédure est valable en toute dimension, pour une combinaison linéaire quelconque de modèles de galiléons généralisés — et même pour leurs extensions de type k-essence (Horndeski et au-delà), c'est-à-dire en remplaçant les coefficients constants de ces modèles par des fonctions du champ scalaire et de son terme cinétique standard, f(φ, ∂μφ∂μφ). En dimension 4, nous retrouvons les 6 classes de modèles exhibés par Gleyzes et al., mais nous les généralisons à toute dimension, et il y a par exemple 30 classes de modèles dans les 10 dimensions de la théorie des cordes.
Nous avons aussi compris les raisons profondes de l'existence de nos deux combinaisons d'équations d'ordre 2 temporel ci-dessus. L'une des raisons est spécifique aux théories de galiléons généralisés, dont les actions peuvent être écrites en termes de contractions avec des tenseurs de Levi-Civita. Leur antisymétrie totale implique en particulier que le tenseur énergie-impulsion du champ scalaire ne dépend d'aucune dérivée troisième de la métrique. Cette information, combinée ensuite à l'invariance de la théorie sous les difféomorphismes, implique l'existence de nos deux combinaisons d'équations, et également le fait que la contraction de ∂t2gij y intervenant a précisément la même forme que les dérivées temporelles troisièmes de la métrique dans les autres équations.
En conclusion, nous confirmons in fine le résultat surprenant de Gleyzes et al., mais nos démonstrations sont profondément différentes. Nous n'avons fixé aucune jauge dans notre analyse hamiltonienne du modèle de galiléon quartique, et nous avons utilisé des équations d'ordre 2 temporel dans notre argument général (en dimension quelconque), sans perdre aucune d'entre elles. Comme souligné ci-dessus, ce second argument n'est pourtant pas une preuve, et les travaux ultérieurs de D. Langlois et K. Noui ont montré que certains modèles possèdent un second degré de liberté scalaire malgré notre réécriture des équations de champs n'employant pas plus de deux dérivées temporelles. Cela souligne que seule l'analyse hamiltonienne complète permet de compter correctement les degrés de liberté.
Notre article [50] a ainsi été le premier de la littérature à réellement démontrer que le modèle de galiléon quartique ne contient qu'un seul degré de liberté scalaire. Les travaux ultérieurs de plusieurs autres équipes sont allés bien au-delà, en simplifiant cette lourde analyse hamiltonienne, et en classifiant tous les modèles possibles selon leur nombre de degrés de liberté. La stabilité de ceux ne contenant qu'un seul scalaire n'est toutefois pas garantie, car cet unique scalaire peut lui-même avoir une énergie cinétique négative, donc chaque modèle spécifique et ses solutions doivent être analysés en détail, aussi bien en cosmologie que pour la physique des trous noirs, des pulsars binaires ou du système solaire. Le chapitre VIII.6 ci-dessous concerne précisément la stabilité d'une solution exacte de trou noir dans un espace-temps de de Sitter.
Plusieurs travaux de la littérature ont montré que certains modèles de galiléons/Horndeski généralisés peuvent prédire un auto-ajustement de la constante cosmologique. Cela signifie qu'une très grande constante cosmologique nue est présupposée être présente dans l'action définissant la théorie (par exemple parce qu'elle est engendrée par les brisures spontanées de symétrie durant l'expansion cosmologique de l'Univers), mais que le tenseur énergie-impulsion du champ scalaire la compense exactement (pour les premiers modèles proposés, tendant donc asymptotiquement vers un espace de Minkowski) ou presque exactement, prédisant alors une très petite constante cosmologique effective compatible avec les données observationnelles.
Au lieu de nous concentrer sur un modèle particulier, nous avons analysé simultanément toutes les théories de Horndeski généralisées dans notre article [51] en collaboration avec E. Babichev. Nous nous sommes toutefois concentrés sur la classe de modèles présentant une symétrie par changement de l'origine du champ scalaire ("shift symmetry"), c'est-à-dire celles dont les six fonctions arbitraires les définissant en dimension 4 ne dépendent que du terme cinétique standard (∂μφ)2 et non du champ scalaire φ lui-même. Les équations de champs à résoudre sont en effet considérablement simplifiées dans cette classe, et un champ scalaire de fond dépendant linéairement du temps fournit notamment une solution.
Notre premier résultat est que cet auto-ajustement n'est pas caractéristique des premiers modèles proposés dans la littérature, mais est au contraire générique. À part pour quelques cas particuliers pathologiques (que nous discutons tous), nous montrons en effet qu'il suffit que le lagrangien du champ scalaire contienne au moins deux termes différents parmi les six possibles, et que le seul paramètre dimensionné dont ils dépendent (disons M) ne soit pas du même ordre de grandeur que la densité d'énergie nue du vide MPlanck2Λnue. La très petite constante cosmologique effective est alors prédite par le modèle comme une puissance du rapport sans dimension M4/(MPlanck2Λnue). Notre premier résultat a donc été de résoudre les équations du fond cosmologique pour tous ces modèles.
Mais nous montrons ensuite que seule une sous-classe d'entre eux peut aussi être compatibles avec les très précis tests de la gravitation post-newtonienne dans le système solaire. Pour cela, nous avons étudié les solutions à symétrie sphérique plongées dans les fonds cosmologiques obtenus ci-dessus. Nous avons établi les relations que doivent satisfaire les fonctions de (∂μφ)2 pour que cette solution soit suffisamment proche de celle de Schwarzschild au voisinage du corps massif. Nous avons aussi identifié une sous-classe de modèles qui prédisent une solution de Schwarzschild-de Sitter exacte, la différence cruciale par rapport à la relativité générale étant que la constante cosmologique intervenant dans la métrique n'est pas Λnue (supposée très grande) mais l'effective engendrée par l'auto-ajustement sus-mentionné. Outre des corps massifs comme le soleil, ces solutions décrivent aussi des trous noirs chevelus, et nous démontrons qu'ils sont réguliers.
Notre troisième résultat est que la constante de Newton est également renormalisée de façon générique dans ces modèles, et la plupart d'entre eux prédisent en fait que le produit MPlanck2Λ observable (effectif) est du même ordre de grandeur que sa valeur nue. C'est un très grave problème pour les modèles d'auto-ajustement, et il suffit pour éliminer ceux proposés auparavant dans la littérature. En effet, bien que la constante cosmologique effective puisse être prédite aussi petite qu'on le désire (en ajustant convenablement l'échelle dimensionnée M dont dépend le lagrangien du champ scalaire), la densité d'énergie du vide reste toujours extrêmement grande par rapport aux observations. Toutefois, nous montrons qu'une sous-sous-classe de modèles (qui reste infinie) ne prédit pas de renormalisation de la constante de Newton. Dans ce cas, l'auto-ajustement de la constante cosmologique correspond bel et bien à une valeur de la densité d'énergie du vide aussi petite que nécessaire.
En conclusion, nous avons identifié un ensemble précis de théories de Horndeski généralisées qui présentent toutes les propriétés désirées : la métrique est presque égale à celle de Schwarzschild au voisinage du soleil, donc les tests classiques de la relativité générale sont satisfaits, et le tenseur énergie-impulsion du champ scalaire compense presque exactement la constante cosmologique nue, en tout point de l'espace-temps, de telle sorte que la densité d'énergie du vide observable soit compatible avec l'expérience.
La lettre [52] et l'article [53], en collaboration avec E. Babichev, C. Charmousis et A. Lehébel, démontrent également plusieurs résultats importants.
Le premier corrige un raisonnement erroné utilisé dans littérature, notamment par plusieurs équipes japonaises. Ces physiciens calculent le hamiltonien de perturbations au voisinage d'une solution de trou noir (dans une théorie précise de galiléons, contenant le terme surnommé "John" dans la classe des "Fab Four"), et trouvent qu'il devient non borné inférieurement lorsqu'on s'approche suffisamment près de l'horizon. Ils en concluent que cette solution est instable. Cependant, ils généralisent de façon abusive le théorème connu, qui garantit que la solution d'énergie minimum est stable quand le hamiltonien est borné inférieurement. La réciproque n'est pas vraie, et nous expliquons en détail pourquoi, dans la première partie de notre article [53]. Comme le hamiltonien n'est pas une quantité scalaire, sa définition dépend du système de coordonnées choisi, et il se combine en fait à d'autres grandeurs conservées correspondant à la quantité de mouvement du système. Dans les théories de galiléons et de Horndeski, les cônes causaux des gravitons et du champ scalaire ne coïncident pas avec celui de la lumière, donc ils peuvent correspondre à des vitesses de propagation inférieures ou supérieures à c. Dans les deux cas, il existe des référentiels suffisamment "boostés" tels que le hamiltonien devienne non borné inférieurement, alors que la théorie et la solution sont pourtant stables — comme le prouve le calcul dans un référentiel convenablement choisi. C'est précisément ce qui se passe lorsque l'on s'approche de l'horizon d'un trou noir en coordonnées de Schwarzschild, comme le font les physiciens sus-mentionnés, mais cela ne prouve en rien que la solution est instable. Nous établissons alors un critère de stabilité correct, qui revient à dire que le hamiltonien est borné inférieurement dans au moins un système de coordonnées. Lorsqu'on se concentre sur les termes cinétiques des perturbations, nous montrons qu'il faut et il suffit que l'ensemble des cônes causaux de tous les champs présents dans la théorie ait à la fois une direction intérieure commune (qui deviendra le temps du "bon" système de coordonnées) et une 3-surface de genre espace, extérieure à tous ces cônes — cette deuxième condition étant également nécessaire pour que le problème de Cauchy soit bien posé.
Ce critère nous permet alors de montrer que la solution de trou noir en question est bel et bien stable pour certaines valeurs des paramètres définissant la théorie. L'instabilité systématique annoncée dans la littérature était donc un simple "effet de coordonnées", sans réalité physique. Notons que le critère erroné utilisé dans la littérature pouvait aussi conduire à conclure à tort qu'une solution était stable. Notre critère correct tient compte de tous les champs présents dans le modèle, donc analyser seulement certains d'entre eux ne permet pas de conclure.
Nos autres résultats concernent la vitesse de propagation des ondes gravitationnelles dans ce modèle de galiléons. La récente détection simultanée des ondes gravitationnelles et électromagnétiques émises lors de la coalescence de deux étoiles à neutrons impose en effet que leurs vitesses doivent être extrêmement proches. Plusieurs articles récents ont identifié quelles théories de Horndeski étendues satisfont un critère d'égalité stricte de ces vitesses, au moins dans un contexte cosmologique décrit par un univers homogène. Il est toutefois important de vérifier que cette égalité reste satisfaite au voisinage de corps massifs, par exemple près d'un trou noir, où la courbure et les gradients du champ scalaire sont grands et où la séparation des degrés de liberté de spin 0 et 2 est difficile. Nous avons pu le prouver pour le modèle de galiléons ci-dessus, en analysant les différents multipôles de ses perturbations, et en choisissant convenablement la métrique difforme à laquelle doit être couplée la matière pour que les ondes électromagnétiques et gravitationnelles se propagent à la même vitesse.
Nous avons par ailleurs montré qu'il reste une classe infinie de modèles de Horndeski étendus qui satisfont cette égalité des vitesses, et conduisent à des modèles cosmologiques auto-ajustant la constante cosmologique à sa très petite valeur observée (comme dans le chapitre VIII.5 ci-dessus). Il était important de le souligner, car beaucoup de collègues pensaient que cette contrainte expérimentale sur la vitesse des ondes gravitationnelles avait sonné la mort de tous ces modèles cosmologiques.
[1] R. Coquereaux et G. Esposito-Farèse, The theory of Kaluza-Klein-Jordan-Thiry revisited, Ann. Inst. H. Poincaré 52 (1990) 113–50.
[2] G. Esposito-Farèse, One-loop divergences of quantized Kaluza-Klein-Jordan-Thiry theory, Prétirage CPT-88/P.2192 (janvier 1989), inclus dans ma thèse [4] (version scannée).
[3] R. Coquereaux et G. Esposito-Farèse, One-loop divergences in quantum gravity: the Einstein-Maxwell-Kaluza-Klein system, Class. Quantum Grav. 7 (1990) 1583–97 (CQG server).
[4] G. Esposito-Farèse, Théorie de Kaluza-Klein et gravitation quantique, Thèse de Doctorat, CPT-89/P.2305 (octobre 1989).
[5] R. Coquereaux et G. Esposito-Farèse, Right-invariant metrics on the Lie group SU(3) and the Gell-Mann-Okubo formula, J. Math. Phys. 32 (1991) 826–31 (version scannée).
[6] R. Coquereaux, G. Esposito-Farèse, G. Vaillant, Higgs fields as Yang-Mills fields and discrete symmetries, Nucl. Phys. B 353 (1991) 689–706 (version scannée).
[7] G. Esposito-Farèse, One-loop divergences in chiral perturbation theory and right-invariant metrics on SU(3), Z. Phys. C 50 (1991) 255–74 (version scannée).
[8] R. Coquereaux, G. Esposito-Farèse, F. Scheck, Noncommutative geometry and graded algebras in electroweak interactions, Int. J. Mod. Phys. A 7 (1992) 6555–93.
[9] G. Esposito-Farèse, Superconnections and noncommutative geometry at the service of the standard model, actes des Journées Relativistes, Cargèse (France), mai 1991, Class. Quantum Grav. 9 (1992) 73–8 (CQG server).
[10] T. Damour et G. Esposito-Farèse, Tensor-multi-scalar theories of gravitation, Class. Quantum Grav. 9 (1992) 2093–176 (CQG server).
[11] G. Esposito-Farèse, Tensor-multi-scalar theories of gravitation and strong-field tests of general relativity, actes des XXVIIes Rencontres de Moriond, janvier 1992, éditions Frontières, 421–6.
[12] T. Damour et G. Esposito-Farèse, Testing local Lorentz invariance of gravity with binary-pulsar data, Phys. Rev. D 46 (1992) 4128–32 (PRD server).
[13] T. Damour et G. Esposito-Farèse, Non-perturbative strong-field effects in tensor-scalar theories of gravitation, Phys. Rev. Lett. 70 (1993) 2220–3 (PRL server).
[14] G. Esposito-Farèse, Non-perturbative strong-field effects in tensor-scalar gravity, actes des XXVIIIes Rencontres de Moriond, février 1993, éditions Frontières, 525–31 (version scannée).
[15] T. Damour et G. Esposito-Farèse, Testing for preferred-frame effects in gravity with artificial Earth satellites, Phys. Rev. D 49 (1994) 1693–706, gr-qc/9311034.
[16] T. Damour et G. Esposito-Farèse, Orbital tests of relativistic gravity using artificial satellites, Phys. Rev. D 50 (1994) 2381–9, gr-qc/9403051.
[17] T. Damour et G. Esposito-Farèse, Testing gravity to second post-Newtonian order: a field-theory approach, Phys. Rev. D 53 (1996) 5541–78, gr-qc/9506063.
[18] T. Damour et G. Esposito-Farèse, Tensor-scalar gravity and binary-pulsar experiments, Phys. Rev. D 54 (1996) 1474–91, gr-qc/9602056.
[19] G. Esposito-Farèse, Binary-pulsar tests of strong-field gravity, conférence plénière au colloque Pulsar Timing, General Relativity, and the Internal Structure of Neutron Stars, Académie Royale des Arts et des Sciences de Hollande, septembre 1996 (actes : Amsterdam, 1999) 13–29, gr-qc/9612039.
[20] T. Damour et G. Esposito-Farèse, Light deflection by gravitational waves from localized sources, Phys. Rev. D 58 (1998) 044003, gr-qc/9802019.
[21] T. Damour et G. Esposito-Farèse, Gravitational-wave versus binary-pulsar tests of strong-field gravity, Phys. Rev. D 58 (1998) 042001, gr-qc/9803031.
[22] G. Esposito-Farèse, Comparing solar-system, binary-pulsar, and gravitational-wave tests of gravity, actes des XXXIVes Rencontres de Moriond, janvier 1999, World Publishers (Hanoï), 475–80, gr-qc/9903058.
[23] G. Esposito-Farèse, General relativity tests: binary pulsars, in Encyclopedia of Astronomy and Astrophysics, éditions Macmillan/IOP, ISBN 1-56159-268-4 (2000).
[24] B. Boisseau, G. Esposito-Farèse, D. Polarski, A.A. Starobinsky, Reconstruction of a scalar-tensor theory of gravity in an accelerating universe, Phys. Rev. Lett. 85 (2000) 2236, gr-qc/0001066.
[25] G. Esposito-Farèse et D. Polarski, Scalar-tensor gravity in an accelerating universe, Phys. Rev. D 63 (2001) 063504, gr-qc/0009034.
[26] G. Esposito-Farèse, Tests of strong-field gravity and gravitational radiation damping in binary-pulsar systems, actes de la 9e conférence Marcel Grossmann, MG9, Rome (Italie), juillet 2000, World Scientific (2002), p. 2041, gr-qc/0011114.
[27] G. Esposito-Farèse, A phenomenological approach to quintessence in scalar-tensor gravity, actes de la 9e conférence Marcel Grossmann, MG9, Rome (Italie), juillet 2000, World Scientific (2002), p. 1749, gr-qc/0011115.
[28] G. Esposito-Farèse, Scalar-tensor theories and Cosmology, & Tests of a quintessence-Gauss-Bonnet coupling, actes des XXXVIIIes Rencontres de Moriond, Les Arcs, mars 2003, Thê' Giói Publishers (Vietnam), 427–34, gr-qc/0306018.
[29] L. Blanchet, T. Damour, G. Esposito-Farèse, Dimensional regularization of the third post-Newtonian dynamics of point particles in harmonic coordinates, Phys. Rev. D 69 (2004) 124007, gr-qc/0311052.
[30] G. Esposito-Farèse, Binary-pulsar tests of strong-field gravity and gravitational radiation damping, actes de la 10e conférence Marcel Grossmann, MG10, Rio de Janeiro (Brésil), juillet 2003, World Scientific (2005), 647–66, gr-qc/0402007.
[31] L. Blanchet, T. Damour, G. Esposito-Farèse, B.R. Iyer, Gravitational radiation from inspiralling compact binaries completed at the third post-Newtonian order, Phys. Rev. Lett. 93 (2004) 091101, gr-qc/0406012.
[32] G. Esposito-Farèse, La relativité générale à l'épreuve des pulsars, Pour la Science 326, décembre 2004, 68–72.
[33] G. Esposito-Farèse, Tests of scalar-tensor gravity, conférence plénière au colloque Phi in the Sky: The Quest for Cosmological Scalar Fields, Porto (Portugal), juillet 2004, AIP Conference Proceedings 736, 35–52, gr-qc/0409081.
[34] L. Blanchet, T. Damour, G. Esposito-Farèse, B.R. Iyer, Dimensional regularization of the third post-Newtonian gravitational wave generation from two point masses, Phys. Rev. D 71 (2005) 124004, gr-qc/0503044.
[35] G. Esposito-Farèse, Tests of alternative theories of gravity, cours donné au 33rd SLAC Summer Institute on Particle Physics, eConf C0507252 SLAC-R-819 (2005) T025, <http://www.slac.stanford.edu/econf/C0507252/papers/T025.PDF>.
[36] J.-P. Bruneton et G. Esposito-Farèse, Field-theoretical formulations of MOND-like gravity, Phys. Rev. D 76 (2007) 124012, arXiv:0705.4043 [gr-qc].
[37] G. Esposito-Farèse, Summary of session A4 at the GRG18 conference: Alternative Theories of Gravity, Class. Quantum Grav. 25 (2008) 114017, arXiv:0711.0332 [gr-qc].
[38] C. Deffayet, G. Esposito-Farèse, A. Vikman, Covariant Galileon, Phys. Rev. D 79 (2009) 084003, arXiv:0901.1314 [hep-th].
[39] G. Esposito-Farèse, Motion in alternative theories of gravity, chapitre du livre Mass and Motion in General Relativity, éd. L. Blanchet, A. Spallici et B. Whiting, série Fundamental Theories of Physics 162 (Springer, Dordrecht, 2011) 461–89, arXiv:0905.2575 [gr-qc].
[40] C. Deffayet, S. Deser, G. Esposito-Farèse, Generalized Galileons: All scalar models whose curved background extensions maintain second-order field equations and stress-tensors, Phys. Rev. D 80 (2009) 064015, arXiv:0906.1967 [gr-qc].
[41] G. Esposito-Farèse, C. Pitrou, J.-P. Uzan, Vector theories in cosmology, Phys. Rev. D 81 (2010) 063519, arXiv:0912.0481 [gr-qc].
[42] C. Deffayet, S. Deser, G. Esposito-Farèse, Arbitrary p-form Galileons, Phys. Rev. D 82 (2010) 061501(R), arXiv:1007.5278 [gr-qc].
[43] Y. Décanini, G. Esposito-Farèse, A. Folacci, Universality of high-energy absorption cross sections for black holes, Phys. Rev. D 83 (2011) 044032, arXiv:1101.0781 [gr-qc].
[44] E. Babichev, C. Deffayet, G. Esposito-Farèse, Improving relativistic modified Newtonian dynamics with Galileon k-mouflage, Phys. Rev. D 84 (2011) 061502(R), arXiv:1106.2538 [gr-qc].
[45] C. Deffayet, G. Esposito-Farèse, R. Woodard, Nonlocal metric formulations of modified Newtonian dynamics with sufficient lensing, Phys. Rev. D 84 (2011) 124054, arXiv:1106.4984 [gr-qc].
[46] E. Babichev, C. Deffayet, G. Esposito-Farèse, Constraints on shift-symmetric scalar-tensor theories with a Vainshtein mechanism from bounds on the time Variation of G, Phys. Rev. Lett. 107 (2011) 251102, arXiv:1107.1569 [gr-qc].
[47] P.C.C. Freire, N. Wex, G. Esposito-Farèse, J.P.W. Verbiest, M. Bailes, B.A. Jacoby, I.H. Stairs, M. Kramer, J. Antoniadis, G.H. Janssen, The relativistic pulsar-white dwarf binary PSR J1738+0333 – II. The most stringent test of scalar-tensor gravity, Mon. Not. R. Astron. Soc. 423 (2012) 3328, arXiv:1205.1450 [astro-ph.GA].
[48] E. Babichev, G. Esposito-Farèse, Time-dependent spherically symmetric covariant Galileons, Phys. Rev. D 87 (2013) 044032, arXiv:1212.1394 [gr-qc].
[49] C. Deffayet, G. Esposito-Farèse, R. Woodard, Field equations and cosmology for a class of nonlocal metric models of MOND, Phys. Rev. D 90 (2014) 064038, arXiv:1405.0393 [astro-ph.CO].
[50] C. Deffayet, G. Esposito-Farèse, D.A. Steer, Counting the degrees of freedom of generalized Galileons, Phys. Rev. D 92 (2015) 084013, arXiv:1506.01974 [gr-qc].
[51] E. Babichev, G. Esposito-Farèse, Cosmological self-tuning and local solutions in generalized Horndeski theories, Phys. Rev. D 95 (2017) 024020, arXiv:1609.09798 [gr-qc].
[52] E. Babichev, C. Charmousis, G. Esposito-Farèse, A. Lehébel, Stability of a black hole and the speed of gravity waves within self-tuning cosmological models, Phys. Rev. Lett. 120 (2018) 241101, arXiv:1712.04398 [gr-qc].
[53] E. Babichev, C. Charmousis, G. Esposito-Farèse, A. Lehébel, Hamiltonian unboundedness vs stability with an application to Horndeski theory, Phys. Rev. D 98 (2018) 104050, arXiv:1803.11444 [gr-qc].
[54] G. Esposito-Farèse, Hamiltonian vs stability in alternative theories of gravity, actes des 54es Rencontres de Moriond, La Thuile, mars 2019, ARISF, 201–8, arXiv:1905.04586 [gr-qc].
[55] E. Babichev, G. Esposito-Farèse, I. Sawicki, L. Trombetta, Large black-hole scalar charges induced by cosmology in Horndeski theories, Phys. Rev. D 112 (2025) 024043, arXiv:2504.07882 [gr-qc].